Using Large Data Sets

طراحی یک سیستم یادگیری با دقت بالا

در این بخش به یکی دیگر از جنبه‌های مهم طراحی سیستم‌های یادگیری ماشین می‌پردازیم و آن پاسخ به سوال "چقدر داده برای آموزش نیاز داریم؟" است.

در بخش‌های قبل در مورد جمع‌آوری داده به صورت کورکورانه هشدار دادیم و گفتیم لزوما داشتن داده زیاد تضمینی برای بهتر کردن الگوریتم یادگیری نیست و گذاشتن وقت زیاد روی آن ممکن است بیهوده باشد. اما در بعضی شرایط خاص (که در مورد آنها بحث خواهیم کرد)، داشتن داده زیاد می‌تواند در به دست‌آوردن یک الگوریتم یادگیری موفق موثر باشد.

بحث را با تحقیق Banko و Brill در سال 2001 آغاز می‌کنیم. این دو نفر سعی در طبقه‌بندی کلمات گیج کننده در انگلیسی داشتند. به عنوان مثال کلماتی مانند too ،to و two که اگر بخواهیم از بین آنها برای کامل کردن جمله زیر انتخاب کنیم:

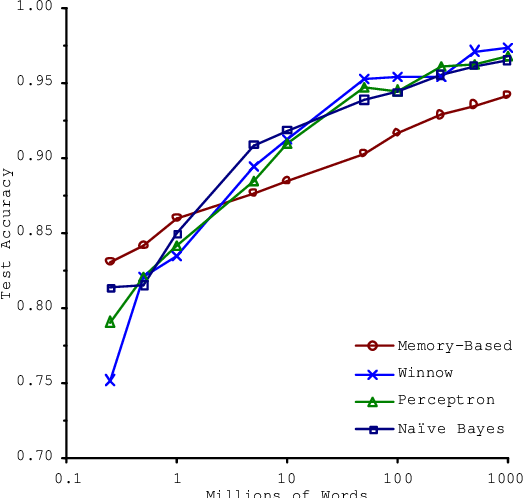
کلمه two را انتخاب خواهیم کرد. اما کاری که آنها انجام دادند استفاده از الگوریتم‌های متفاوت و سپس مشاهده عملکرد آنها با افزایش داده بود. نتیجه کار آنها در نمودار زیر قابل مشاهده است.

در این نمودار دو نکته مهم وجود دارد:

1. الگوریتم‌ها بسیار مشابه عمل می‌کنند.
2. با افزایش تعداد داده عملکرد الگوریتم‌ها بهتر می‌شود.

بعد از این مثال تاثیرگذار، کارهای بسیار دیگری در این زمینه انجام شد. که نتایج مشابهی را هم بیان می‌کردند؛ الگوریتم‌های متفاوت البته با توجه به یک سری جزئیات عملکردهای مشابهی دارند ولی چیزی که می‌تواند الگوریتم را واقعا بهبود ببخشد تعداد داده بیشتر است و نتایج این چنینی باعث شد که در یادگیری ماشین این جمله مشهور بیان شود:

کسی که بهترین الگوریتم را دارد برنده نمی‌شود بلکه کسی برنده می‌شود که بیشترین داده را دارد.

ولی مسئله این است که جمله بالا در چه زمان‌هایی درست است و در چه زمان‌هایی درست نیست؟

منطق استفاده از مجموعه داده‌های بزرگ

برای اینکه بفهمیم چگونه و چه زمانی مجموعه د اده بزرگ می‌تواند به بهبود الگوریتم یادگیری کمک کند بیاید فرض‌هایی را در نظر بگیریم.

ابتدا فرض می‌کنیم که خصوصیت \(x \in \mathbb{R}^{n+1}\) دارای اطلاعات کافی جهت پیش‌بینی \(y\) به صورت دقیق است. برای مثال به کلمات گیج کننده برمی‌گردیم. اگر خصوصیت \(x\) یکی از کلمات اطراف کلمه گیج کننده را تشخیص دهد از روی آن به احتما زیاد می‌تواند به درستی \(y\) را یش‌بینی کند. مثلا در جمله زیر با توجه به کلمات ate و eggs تشخیص کلمه two امکان‌پذیر است و الگوریتم می‌تواند تشخیص دهد کلمات to و too برای این جمله مناسب نیستند.

در برابر این مثال، مثال پیش‌بینی قیمت خانه را در نظر بگیرید که تنها بر اساس یک خصوصیت (اندازه خانه) صورت گیرد. یعنی مثلا به شما بگویند خانه‌ای داریم با مساحت 300 متر مربع قیمت آن را پیش‌بینی کنید و هیچ اطلاعات دیگری از جمله اینکه خانه در کدام منطقه شهر واقع است، قدیمی است یا نوساز، دارای چند اتاق است و ... به شما ندهند. واضح است که خیلی مشکل است بتوانید به درستی و تنها بر اساس اندازه خانه قیمت آن را پیش‌بینی کنید. پس این مثال برخلاف فرض اول ما است که خصوصیت \(x\) اطلاعات کافی جهت پیش‌بینی \(y\) را با دقت دلخواه ما داشته باشد.

با توجه به توضیحات بالا، می‌توان یک آزمایش مفید را انجام داد: با داشتن ورودی \(x\) (اطلاعاتی که برای الگوریتم فراهم کرده‌ایم) آیا یک انسان متخصص می‌تواند با اطمینان \(y\) را پیش‌بینی کند؟

در مورد مثال اول اگر شخص بتواند به خوبی انگلیسی حرف بزند می‌تواند بر اساس اطلاعات داده شده جای خالی را با اطمینان بوسیله کلمه two پر کند. ولی در مورد مثال پیش‌بینی قیمت خانه تنها بر اساس اندازه آن، اگر پیش یک متخصص مشاور املاک برویم نمی‌تواند با اطمینان به ما بگوید که قیمت خانه چقدر است و اگر یک انسان خبره نتواند چگونه انتظار داشته باشیم که الگوریتم یادگیری بتواند؟ هر چقدر هم تعداد داده‌ زیاد باشد.

حال فرض کنیم که خصوصیات ما اطلاعات کافی جهت پیش‌بینی مقدار \(y\) را دارد:

• از الگوریتمی استفاده کنید که تعداد پارامترهای زیادی دارد (رگرسیون خطی/لجستیک با تعداد زیادی خصوصیت یا شبکه عصبی با تعداد زیادی لایه مخفی). به عبارت دیگر الگوریتمی داریم که low bias است. در این حالت می‌دانیم که \(J_{train}(\theta)\) کوچک خواهد بود.
• از یک مجموعه داده عظیم استفاده کنید. با این کار احتمال overfit شدن را غیرمحتمل می‌کنیم. به عبارت دیگر امیدوار خواهیم بود که خطاهای آموزش و آزمایش تقریبا با هم برابر باشند:
  $$J_{train}(\theta) \approx J_{test}(\theta)$$
  به عبارت دیگر خطای \(J_{test}(\theta)\) هم کم خواهد بود.

پس اگر بخواهیم جمع‌بندی داشته باشیم که چه زمانی مجموعه داده زیاد می‌تواند کمک کننده باشد، باید دو شرط زیر را بررسی کنیم:

1. آیا خصوصیات ما اطلاعات کافی جهت پیش‌بینی مقدار \(y\) را دارند؟ به عبارت دیگر می‌توانیم الگوریتمی طراحی کنیم که low bias باشد؟
2. آیا می‌توانیم به مجموعه داده عظیم دسترسی داشته باشیم به طوری که الگوریتم low variance باشد؟

و مهم آن است که این دو شرط با هم وجود داشته باشند.