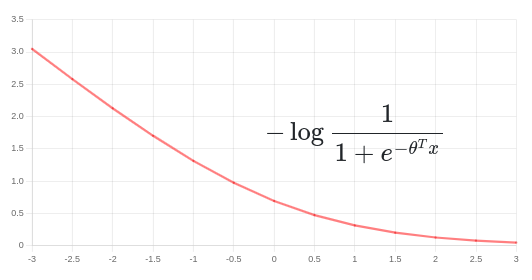Support Vector Machine

معرفی الگوریتم Support Vector Machine

تا اینجا با تعداد متفاوتی از الگوریتم‌های یادگیری با نظارت آشنا شدیم و دیدم که عملکرد آن‌ها تا حد زیادی مشابه یکدیگر است. بنابراین آنچه که بیش از انتخاب الگوریتم مهم است، انتخاب حجم داده‌ و همچنین مهارت فرد در به کار بردن الگوریتم (انتخاب خصوصیت‌ها، پارامتر منظم‌سازی و ...) می‌باشد. با وجود این در این بخش قصد داریم الگوریتم قدرتمند دیگری در حوزه یادگیری با نظارت را که هم در صنعت و هم در بخش آکادمی به صورت گسترده‌ای استفاده می‌شود، معرفی کنیم. این الگوریتم Support Vector Machine (SVM) نام دارد و در مقایسه با رگرسیون لجستیک و شبکه‌های عصبی، بعضی اوقات راه ساده‌تر و بهتری را برای یادگیری توابع پیچیده‌ و غیرخطی فراهم می‌کند. بنابراین در این قسمت با اشاره به این نکته که این آخرین الگوریتم یادگیری با نظارت خواهد بود که به صورت مفصل آن را به بحث خواهیم گذاشت، به معرفی این الگوریتم می‌پردازیم.

برای توضیح در مورد الگوریتم SVM ابتدا بحث را با رگرسیون لجستیک آغاز می‌کنیم و نشان خواهیم داد که چگونه با کمی تغییر در آن به الگوریتم SVM می‌رسیم.

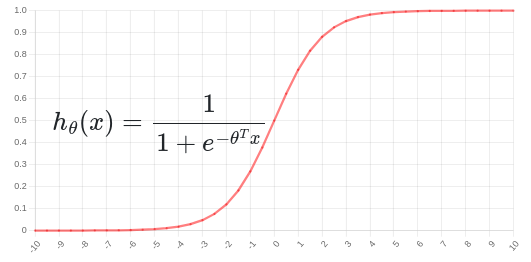
آنچه که از الگوریتم Logistic Regression می‌خواهیم به قرار زیر است:

$$ \text{ If } y = 1, \text{ we want } h_{\theta}(x) \approx 1, \quad \theta^{T}x \gg 0 $$

$$ \text{ If } y = 0, \text{ we want } h_{\theta}(x) \approx 0, \quad \theta^{T}x \ll 0 $$

به عبارت دیگر اگر به نمودار رسم شده در بالا دقت کنید، مشاهده خواهید کرد که هنگامیکه $\theta^{T}x \gg 0$ نمودار به مقدار یک بسیار نزدیک می‌شود، و این همان چیزی است که ما انتظار داریم، یعنی زمانی که داده ما دارای جواب درست $$y = 1$$ است، تابع فرضیه ما هم جواب درست را برابر یک پیش‌بینی کند و همچنین زمانی که داده واقعی جواب درست را $$y = 0$$ معرفی می‌کند، تابع فرضیه ما هم جواب درست را برابر صفر پیش‌بینی کند و این زمانی محقق خواهد شد که $\theta^{T}x \ll 0$ باشد.

بررسی رگرسیون لجستیک از یک منظر دیگر: اگر تابع هزینه رگرسیون لجستیک را تنها برای یک داده بنویسیم، به قرار زیر خواهد بود:

$$ -(y\log h_{\theta}(x) + (1 - y)\log (1 - h_{\theta}(x))) $$

که با جایگذاری مقدار $h_{\theta}(x)$ در آن خواهیم داشت:

$$ -y\log \frac{1}{1+e^{-\theta^{T}x}} - (1 - y)\log (1 - \frac{1}{1+e^{-\theta^{T}x}})$$

حال دو حالت را بررسی می‌کنیم. در حالت اول زمانیکه $$y = 1$$ است، برای این داده تنها جمله اول در تابع هزینه شرکت می‌کند و نمودار آن به شکل زیر خواهد بود:

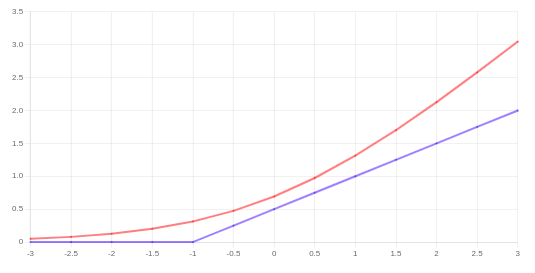
با دقت در نمودار متوجه می‌شویم که با افزایش مقدار $\theta^Tx$ مقدار این جمله (جمله اول در تابع هزینه) به سمت صفر میل می‌کند. در حقیقت از روی این نمودار می‌توان بهتر درک کرد که در حالت $$y = 1$$ ، با افزایش عبارت $\theta^Tx$ مقدار تابع هزینه کاهش می‌یابد (مینیمم شدن تابع هزینه).

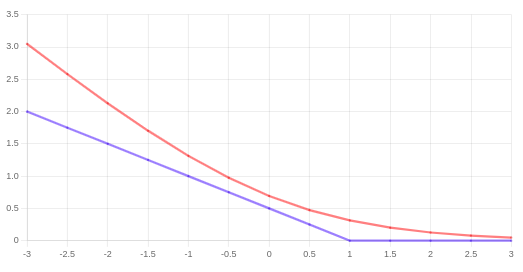
حال می‌خواهیم، کمی این تابع را تغییر دهیم. به شکل زیر دقت کنید:

نمودار آبی رنگ رسم شده تقریب خوبی برای نمودار اصلی (قرمز رنگ) است. نمودار آبی رنگ از دو بخش تشکیل شده؛ زمانیکه مقدار محور افقی بیشتر از یک است، یک خط صاف برابر با مقدار صفر و قسمت دیگر یک خط مستقیم است (شیب آن مهم نیست) که با حرکت به سمت مقادیر کمتر روی محور افقی، مقدار آن افزایش می‌یابد. بنابراین عملکرد 2 نمودار آبی و قرمز مشابه هم هستند ولی در ادامه خواهیم دید نمودار آبی رنگ که تابع هزینه جدید ما در حالت $$y = 1$$ خواهد بود، باعث می‌شود روش SVM برتری محاسباتی داشته باشد و مسئله بهینه‌سازی را برایمان ساده‌تر خواهد کرد.

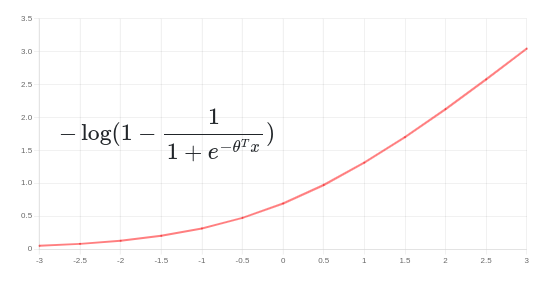
در حالت دوم، زمانیکه $$y = 0$$ است، تنها جمله دوم در تابع هزینه مشارکت خواهد داشت. با دقت در نمودار زیر متوجه خواهیم شد که در اینجا با افزایش مقدار محور افقی ( $\theta^Tx$ ) مقدار تابع هزینه هم افزایش می‌یابد و با کاهش آن و میل به سمت صفر، مقدار تابع هزینه هم به سمت صفر میل می‌کند. به همین جهت، در صورتی که $$y = 0$$ باشد، می‌بایست مقدار $\theta^Tx$ نیز بسیار کوچک باشد.

مشابه با حالت $$y = 1$$ ، تابع هزینه را اصلاح می‌کنیم (نمودار آبی رنگ در شکل زیر). حال به توابع هزینه اصلاح شده به ترتیب اسم‌های $$cost_1(z)$$ و $$cost_0(z)$$ را می‌دهیم، که در آن زیروندهای 1 و صفر به ترتیب به حالت‌های $$y = 1$$ و $$y = 0$$ اشاره دارند و $$z$$ همان $\theta^Tx$ است.

با این نامگذاری، تابع هزینه جدید را برای الگوریتم SVM به شکل زیر در چند مرحله تعریف کنیم. ابتدا معادله مربوط به رگرسیون لجستیک را می‌نویسیم:

$$\begin{eqnarray} \min_{\theta} \frac{1}{m} && \sum_{i = 1}^{m} \left[y^{(i)}\left(-\log h_{\theta}(x^{(i)}) \right) \right. \\ &+&\left. (1 - y^{(i)}) \left(-\log h_{\theta}(x^{(i)}) \right)\right] \\ &+& \frac{\lambda}{2m} \sum_{j = 1}^{n} \theta_{j}^{2} \end{eqnarray}$$

$$ \min_{\theta} \frac{1}{m} \left[\sum_{i = 1}^{m} y^{(i)}\left(-\log h_{\theta}(x^{(i)}) \right) + (1 - y^{(i)}) \left(-\log h_{\theta}(x^{(i)}) \right) \right] + \frac{\lambda}{2m} \sum_{j = 1}^{n} \theta_{j}^{2} $$

سپس بر اساس مطالب گفته شده در بالا توابع $$cost_1(z)$$ و $$cost_0(z)$$ را جایگزین می‌کنیم:

$$\begin{eqnarray} \min_{\theta} \frac{1}{m} && \sum_{i = 1}^{m} \left[y^{(i)}cost_{1}(\theta^Tx^{(i)}) \right. \\ &+& \left. (1 - y^{(i)}) cost_{0}(\theta^Tx^{(i)})\right] \\ &+& \frac{\lambda}{2m} \sum_{j = 1}^{n} \theta_{j}^{2} \end{eqnarray}$$

$$ \min_{\theta} \frac{1}{m} \left[\sum_{i = 1}^{m} y^{(i)}cost_{1}(\theta^Tx^{(i)}) + (1 - y^{(i)}) cost_{0}(\theta^Tx^{(i)})\right] + \frac{\lambda}{2m} \sum_{j = 1}^{n} \theta_{j}^{2} $$

در مرحله بعد ابتدا پارامتر m در مخرج کسرها را حذف می‌کنیم. اگر با ریاضیات مربوط به پیدا کردن نقاط اکسترمم یک تابع آشنا باشید، می‌توانید تایید کنید که ضریب تابع در به دست آوردن نتقاط اکسترمم نقشی بازی نمی‌کند و در هر دو حالت به یک جواب می‌رسیم.

$$\begin{eqnarray} \min_{\theta} && \sum_{i = 1}^{m} \left[y^{(i)}cost_{1}(\theta^Tx^{(i)}) \right. \\ &+& \left. (1 - y^{(i)}) cost_{0}(\theta^Tx^{(i)})\right] \\ &+& \frac{\lambda}{2} \sum_{j = 1}^{n} \theta_{j}^{2} \end{eqnarray}$$

$$\min_{\theta} \left[\sum_{i = 1}^{m} y^{(i)}cost_{1}(\theta^Tx^{(i)}) + (1 - y^{(i)}) cost_{0}(\theta^Tx^{(i)})\right] + \frac{\lambda}{2} \sum_{j = 1}^{n} \theta_{j}^{2} $$

همچنین مرسوم است که به جای $\lambda$ یا همان پارامتر منظم‌سازی از پارامتر دیگری استفاده کنیم. برای معرفی این پارامتر عبارت تابع هزینه بالا را به صورت دو جمله در نظر بگیرید. اگر جمله اول را با حرف A و جمله دوم را بدون $\lambda$ با حرف B نمایش دهیم، می‌توان نوشت:

$$ A + \lambda B $$

و همان‌طور که می‌دانید با انتخاب مقادیر مختلف برای پارامتر ‌ $\lambda$ می‌توان انتخاب کرد که چقدر خوب داده‌ها را برازش کرد و یا چقدر مقادیر پارامترها را کوچک نگه داشت. در SVM مرسوم است که عبارت فوق به شکل زیر نوشته شود:

$$ C A + B $$

که ضریب C به نوعی همان نقش پارامتر منظم‌سازی را دارد. یعنی با انتخاب مقادیر کوچک برای آن، وزن کمتری برای A انتخاب کرده‌ایم و عبارت ‌B غالب خواهد شد (به مانند زمانی که $\lambda$ را بزرگ انتخاب می‌کردیم.) و برعکس. بنابراین می‌توانید تصور کنید که پارامتر جدید معرفی شده نقش عکس لامبدا را دارد ( $C = \frac{1}{\lambda}$ ).

بنابراین تابع هزینه برای SVM به قرار زیر خواهد بود:

$$\begin{eqnarray} \min_{\theta} &C& \sum_{i = 1}^{m} \left[y^{(i)}cost_{1}(\theta^Tx^{(i)}) \right. \\ &+& \left. (1 - y^{(i)}) cost_{0}(\theta^Tx^{(i)})\right] \\ &+& \frac{1}{2} \sum_{j = 1}^{n} \theta_{j}^{2} \end{eqnarray}$$

$$ \min_{\theta} C \sum_{i = 1}^{m} \left[y^{(i)}cost_{1}(\theta^Tx^{(i)}) + (1 - y^{(i)}) cost_{0}(\theta^Tx^{(i)})\right] + \frac{1}{2} \sum_{j = 1}^{n} \theta_{j}^{2} $$

دقت داشته باشید که تابع هزینه معرفی شده، منجر به تابع فرضیه‌ای خواهد شد که به شکل زیر عمل می‌کند:

$$ h_{\theta}(x) = \begin{cases} 1 \quad \quad if \quad \quad \theta^Tx \ge 0 \\ 0 \quad \quad otherwise \end{cases}$$

یعنی برخلاف رگرسیون لجستیک احتمال را بیان نمی‌کند و خروجی آن تنها یکی از دو حالت ممکن خواهد بود.

<< مبحث قبلی مبحث بعدی >>