Principal Component Analysis

معرفی PCA

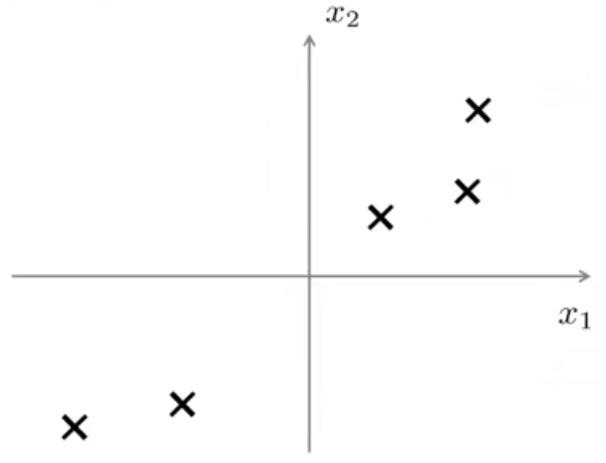
فرض کنید یک مجموعه داده به شکل زیر داریم و می‌خواهیم این مجموعه داده را از 2 بعد به یک بعد کاهش دهیم.

یعنی می‌خواهیم خطی پیدا کنیم که داده‌ها را روی آن تصویر نماییم. خط رسم شده در شکل زیر به نظر می‌رسد که انتخاب معقولی باشد.

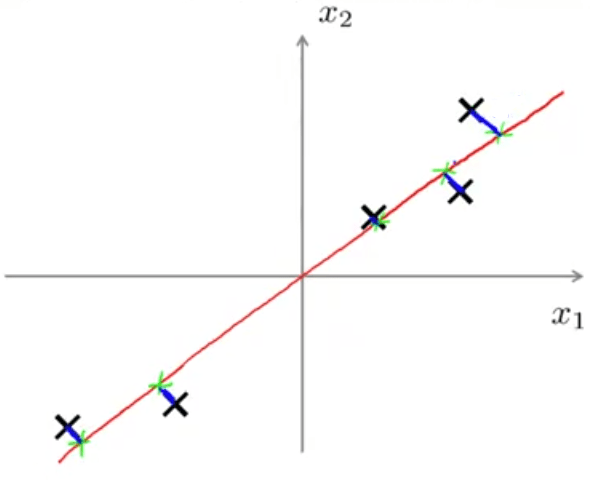
دلیل معقول بودن آن هم به این جهت است که بعد از تصویر کردن داده‌ها روی آن می‌توانیم مشاهده کنیم که فاصله‌ هر داده تا خط رسم شده بسیار کم است. پس در حقیقت PCA دنبال پیدا کردن یک بعد پایین‌تر است (در این مورد یک خط) تا داده‌های تصویر شده روی آن به گونه‌ای باشند که جمع مربع خطوط آبی رنگ کمینه شود. گاهی به طول خطوط آبی رنگ خطای تصویر کردن هم گفته می‌شود.

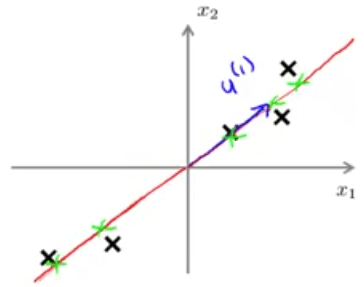
اگر بخواهیم به صورت رسمی‌تر PCA را بیان کنیم، برای حالتی که کاهش بعد را از 2 بعد به یک بعد انجام می‌دهیم می‌توان گفت: جهتی را پیدا کن (یک بردار $u^{(1)} \in \mathbb{R}^n$ ) تا داده‌ها را روی آن به‌گونه‌ای تصویر کنیم که خطای تصویر کردن کمینه شود.

دقت داشته باشید که اگر PCA بردار $-u^{(1)}$ را هم به ما بدهد فرقی نمی‌کند؛ یعنی آنچه که برای ما مهم است راستای بردار است نه جهت آن. در حالت کلی‌تر وقتی که می‌خواهیم $$n$$ بعد را به $$k$$ بعد کاهش دهیم تعریف PCA چنین خواهد بود:

\(k\)

بردار

u^{(1)},...,u^{(k)}

را چنان پیدا کن که با تصویر کردن داده‌ها روی آن‌ها خطای تصویر کردن کمینه شود.

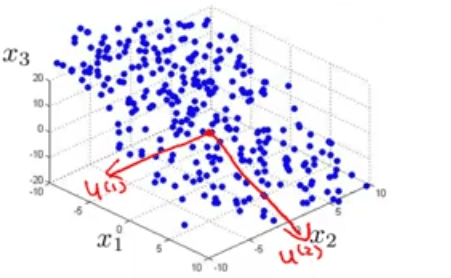
مثلا اگر بخواهیم حالت $$3D$$ را به $$2D$$ کاهش دهیم نیاز به 2 بردار داریم. این 2 بردار یک سطح را تعریف می‌کنند که می‌توانیم داده‌ها را چنان روی آن تصویر کنیم که خطای تصویر کمینه شود.

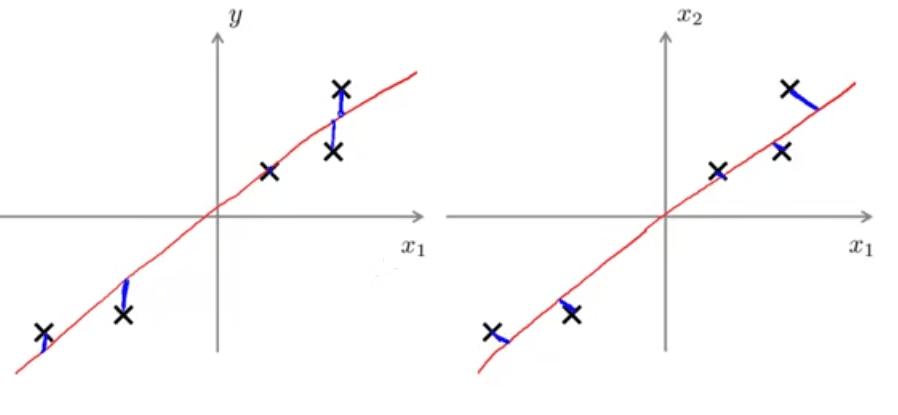
نکته آخر در این بخش اینکه دقت داشته باشید PCA و رگرسیون خطی هر چند بسیار مشابه به‌نظر می‌رسند ولی دو چیز کاملا متفاوت هستند. در رگرسیون خطی ما به دنبال پیش‌بینی متغیری مثل $$y$$ براساس داده‌های ورودی $$x$$ هستیم. به عنوان نمونه رگرسیون خطی در شکل سمت چپ به دنبال برازش دادن خطی به داده‌هاست که مجموع مربع خطاها (یعنی اختلاف داده‌ها با خط رسم شده) کمینه شود. خطوط آبی رنگ رسم شده بر خط قرمز عمود هستند. در حالیکه PCA در شکل سمت راست، دنبال کمینه کردن اندازه‌ خطوط آبی رنگ که با زاویه رسم شده‌اند (کمترین فاصله) می‌باشد. همچنین هیچ متغیر ویژه‌ای به مانند $$y$$ که در رگرسیون خطی به دنبال پیش‌بینی آن هستیم وجود ندارد و تنها یکسری متغیر $$x_1,...,x_n$$ وجود دارند که همه‌ آن‌ها یکسان هستند و هیچ کدام ویژه نیستند.

الگوریتم PCA

قبل از پیاده‌سازی الگوریتم PCA یک گام پیش پردازش داده‌ها را باید انجام دهیم. این گام شامل نرمالیزه کردن میانگین و در صورت لزوم مقیاس کردن خصوصیات است. به این معنی که اگر مجموعه داده‌ $x^{(1)},...,x^{(m)}$ را داشته باشیم ابتدا میانگین داده‌ها را محاسبه می‌کنیم:

$$ \mu_j = \frac{1}{m} \sum_{i=1}^{m} x^{(i)}_{j} $$

سپس هر داده $x^{(i)}_{j}$ را با $x_j - \mu_j$ جایگزین می‌کنیم. در صورتی که خصوصیت‌های متفاوت ما دارای مقیاس‌های متفاوتی باشند (مثلا $$x_1$$ اندازه خانه و $$x_2$$ تعداد اتاق‌ها باشد) باید خصوصیت‌ها را مقیاس کنیم تا در محدوده‌ای قابل مقایسه قرار گیرند:

$$ \frac{x^{(i)}_{j} - \mu_j}{s_j} $$

$$s_j$$ می‌تواند اختلاف بیشترین و کمترین مقدار خصوصیت و یا انتخاب رایج یعنی انحراف معیار باشد.

الگوریتم PCA برای کاهش از $$n$$ بعد به $$k$$ بعد:

محاسبه ماتریس کوواریانس:

$$ \Sigma = \frac{1}{m} \sum_{i=1}{m} \left(x^{(i)}\right)\left(x^{(i)}\right)T $$

محاسبه ویژه بردارهای ماتریس کوواریانس:

$$ U,S,V = np.linalg.svd(\Sigma) $$

در کد پایتون بالا svd مخفف کلمات Singular Vector Decomposition و به معنی تجزیه به مقادیر تکین است. در اینجا وارد بحث ریاضیاتی نمی‌شویم و تنها دانستن نحوه‌ محاسبه ویژه‌ بردارها توسط پایتون برای هدف ما کفایت می‌کند. چنانچه ملاحظه می‌کنید دستور svd سه ماتریس را برمی‌گرداند که ما تنها ماتریس U را می‌خواهیم. U یک ماتریس $n \times n$ است که ستون‌های آن همان بردارهایی هستند که به دنبال آن بودیم.

جهت محاسبه ویژه بردارهای یک ماتریس از تابع eig() استفاده می‌شود. ولی از آنجایی که ثابت می‌شود که ماتریس کوواریانس همواره یک ماتریس متقارن مثبت معین است، تابع svd هم همان نتیجه تابع eig() را برای آن برمی‌گرداند.

$$ U = \begin{bmatrix} | & | & | & & | \\ u^{(1)} & u^{(2)} & u^{(3)} & ... & u^{(n)} \\| & | & | & & | \end{bmatrix} \in \mathbb{R}^{n \times n} $$

حال برای کاهش بعد از $x \in \mathbb{R}^n$ به $z \in \mathbb{R}^k$ باید $$k$$ ستون اول از ماتریس $$U$$ را انتخاب کنیم:

$$ U_{\text{reduce}} = \begin{bmatrix} | & | & | & & | \\ u^{(1)} & u^{(2)} & u^{(3)} & ... & u^{(k)} \\| & | & | & & | \end{bmatrix} \in \mathbb{R}^{n \times k} $$

و در نهایت برای محاسبه خصوصیت‌های جدید کافی است به شکل زیر عمل کنیم:

$$ Z = U^{T}_{\text{reduce}} X $$

<< مبحث قبلی مبحث بعدی >>