Multivariate Gaussian Distribution

توزیع گاوسین چند متغیره

در این بخش می‌خواهیم در مورد توسعه الگوریتم یافتن بی‌هنجاری که تا کنون ساخته‌ایم، بحث کنیم. این توسعه که با اسم توزیع گاوسین چند متغیره هم شناخته می‌شود دارای یک سری مزایا و معایب است و گاهی اوقات می‌تواند به ما در یافتن برخی بی‌هنجاری‌ها کمک کند. به مثال زیر که در ارتباط با رصد کردن کامپیوترهای مرکز داده است توجه کنید.

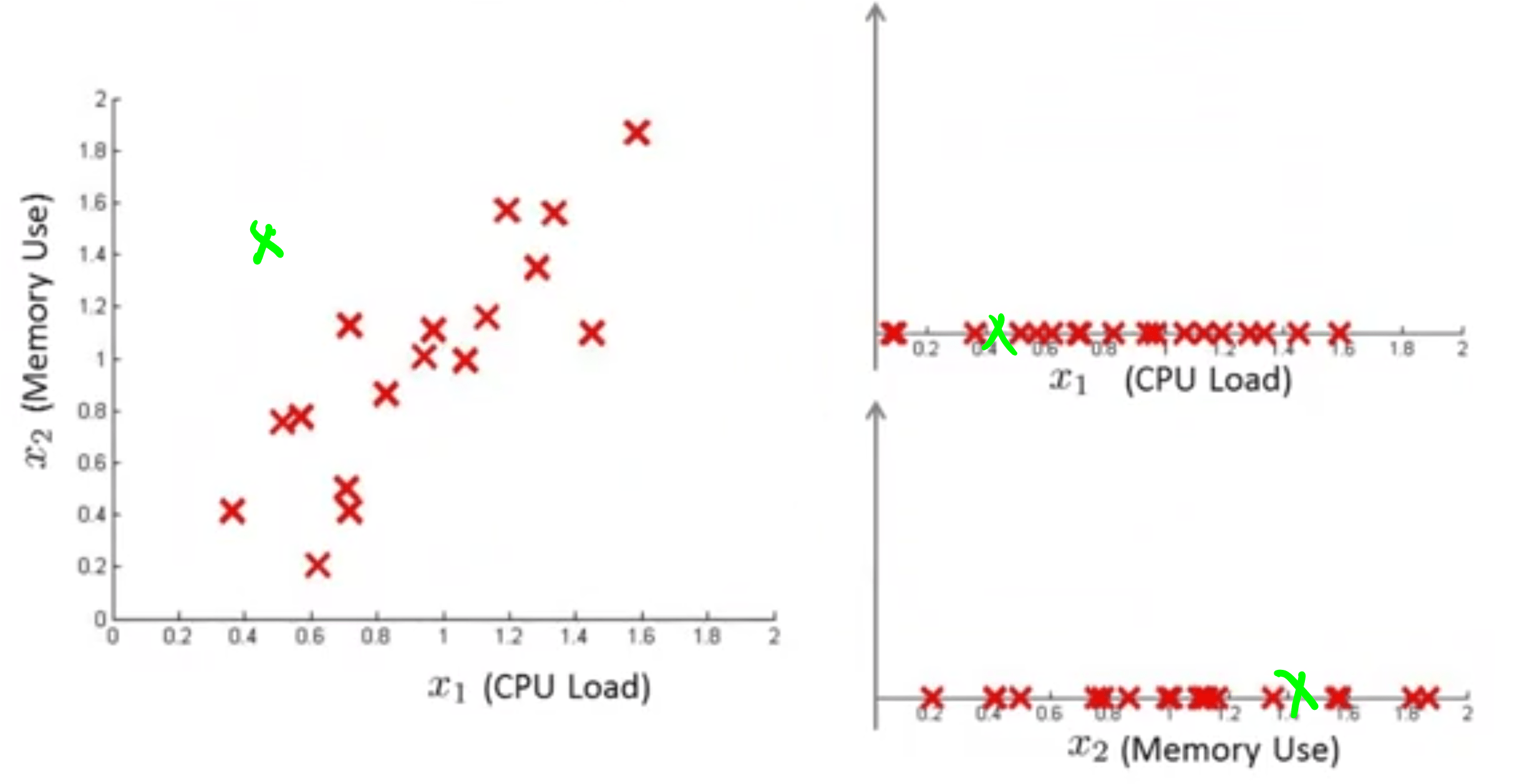
دو خصوصیت رسم شده در زیر یکی بارگذاری CPU و دیگری استفاده از حافظه است.

شکل سمت چپ تقریبا یک ارتباط خطی را بین دو خصوصیت نشان می‌دهد. یعنی با افزایش بارگذاری CPU استفاده از حافظه هم بیشتر می‌شود و بر این اساس ضربدر سبز رنگ مشخص شده می‌بایست بی‌هنجار باشد در حالیکه بارگذاری CPU کم و استفاده از حافظه زیاد است. حال ببینیم الگوریتم ساخته شده یافتن بی‌هنجاری این نقطه را چگونه تشخیص می‌دهد؟

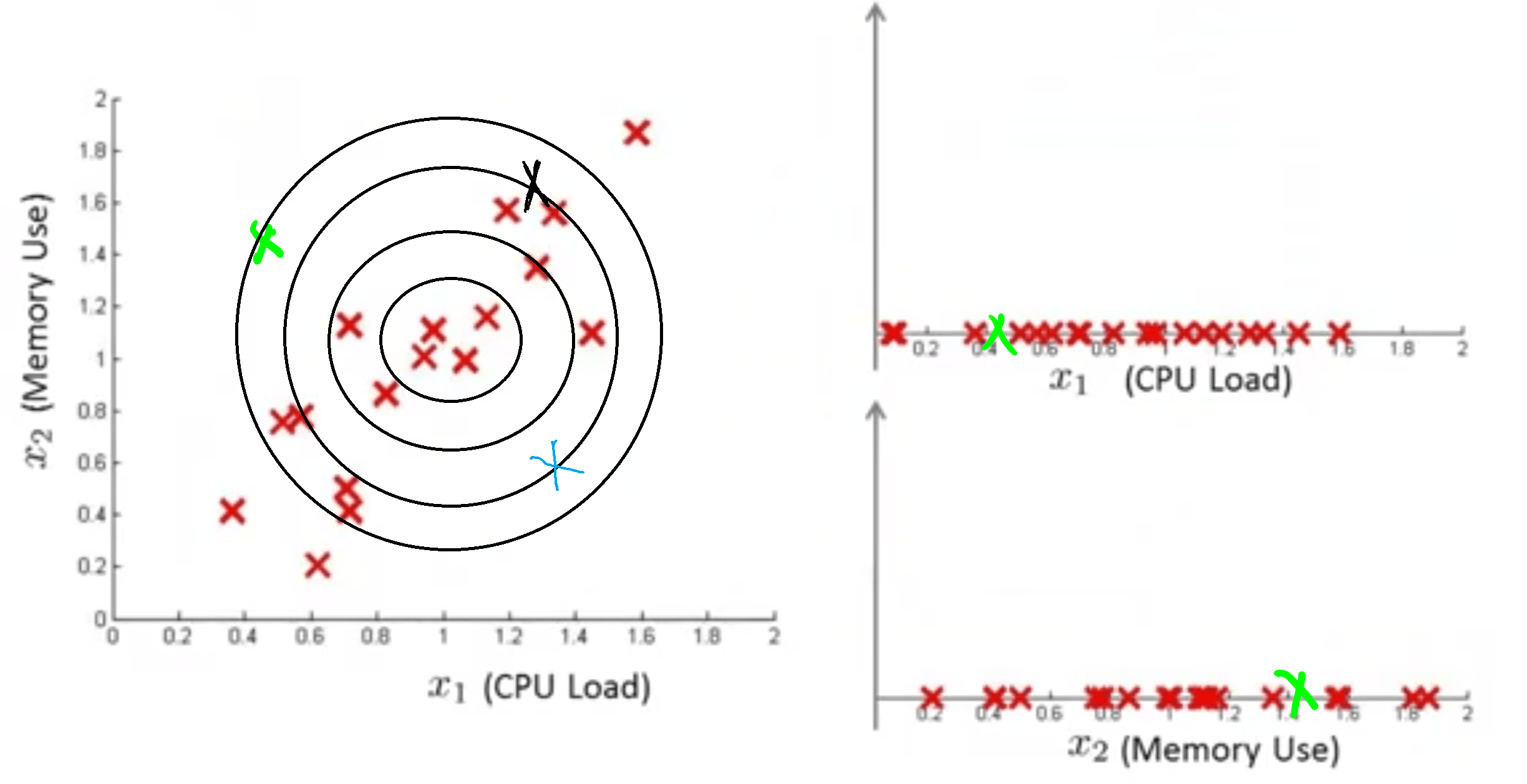
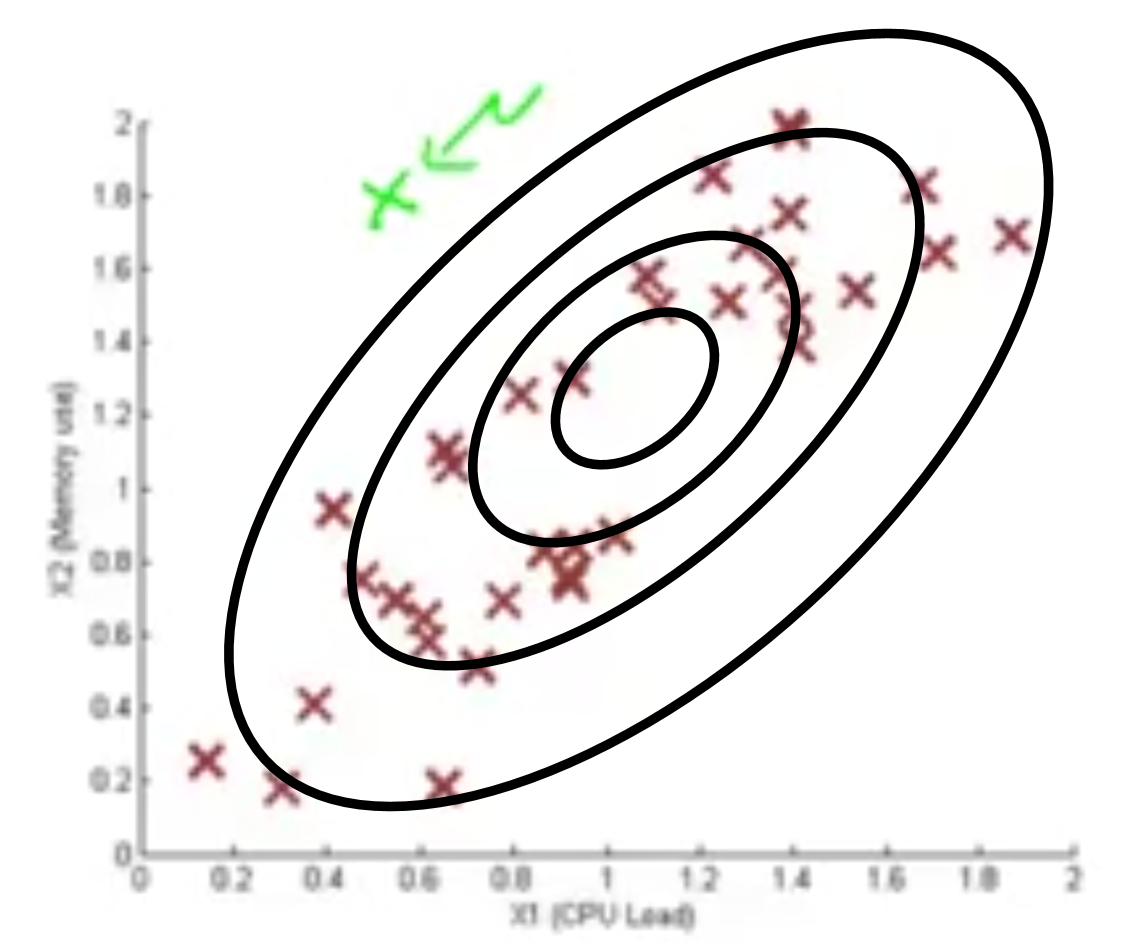
روی نمودارهای سمت راست ضربدر سبز رنگ برای هر دو خصوصیت نشان داده شده است. مشاهده می‌کنیم که در هیچکدام از خصوصیت‌ها این نقطه بی‌هنجار به نظر نمی‌رسد و در نتیجه الگوریتم یافتن بی‌هنجاری در تشخیص این نقطه به عنوان نمونه بی‌هنجار شکست می‌خورد. برای روشن شدن موضوع به شکل زیر نگاه کنید:

چنانکه می‌دانید دایره‌های رسم شده میزان احتمال نرمال بودن نمونه را نشان می‌دهند. به این صورت که هر چقدر از دایره مرکزی به سمت دایره‌های بیرونی حرکت کنیم، احتمال نرمال بودن کاهش می‌یابد. مشکلی که وجود دارد این است که الگوریتم تفاوتی بین نقاط آبی و مشکی مشخص شده روی نمودار به لحاظ احتمالاتی قائل نمی‌شود، به عبارتی احتمال نرمال بودن هر دو را برابر در نظر می‌گیرد. در حالیکه واضح است نقطه آبی رنگ می‌بایست احتمال بسیار کمتری داشته باشد و بی‌هنجار تشخیص داده شود.

برای حل این مشکل سراغ توزیع گاوسین (نرمال) چند متغیره می‌رویم. فرض کنید $x \in \mathbb{R}^n$ . به جای مدل کردن $$p(x_1), p(x_2), ...$$ به صورت جداد جدا، همه $$p(x)$$ ها را در یک حرکت (همزمان) مدل می‌کنیم. در این حالت پارامترهای ما عبارتند از:

$$ \mu \in \mathbb{R}^n$$

$$\Sigma \in \mathbb{R}^{n \times n}$$

که $\Sigma$ ماتریس کوواریانس است. بر اساس این پارامترها فرمول توزیع نرمال چند متغیره به صورت زیر نوشته می‌شود:

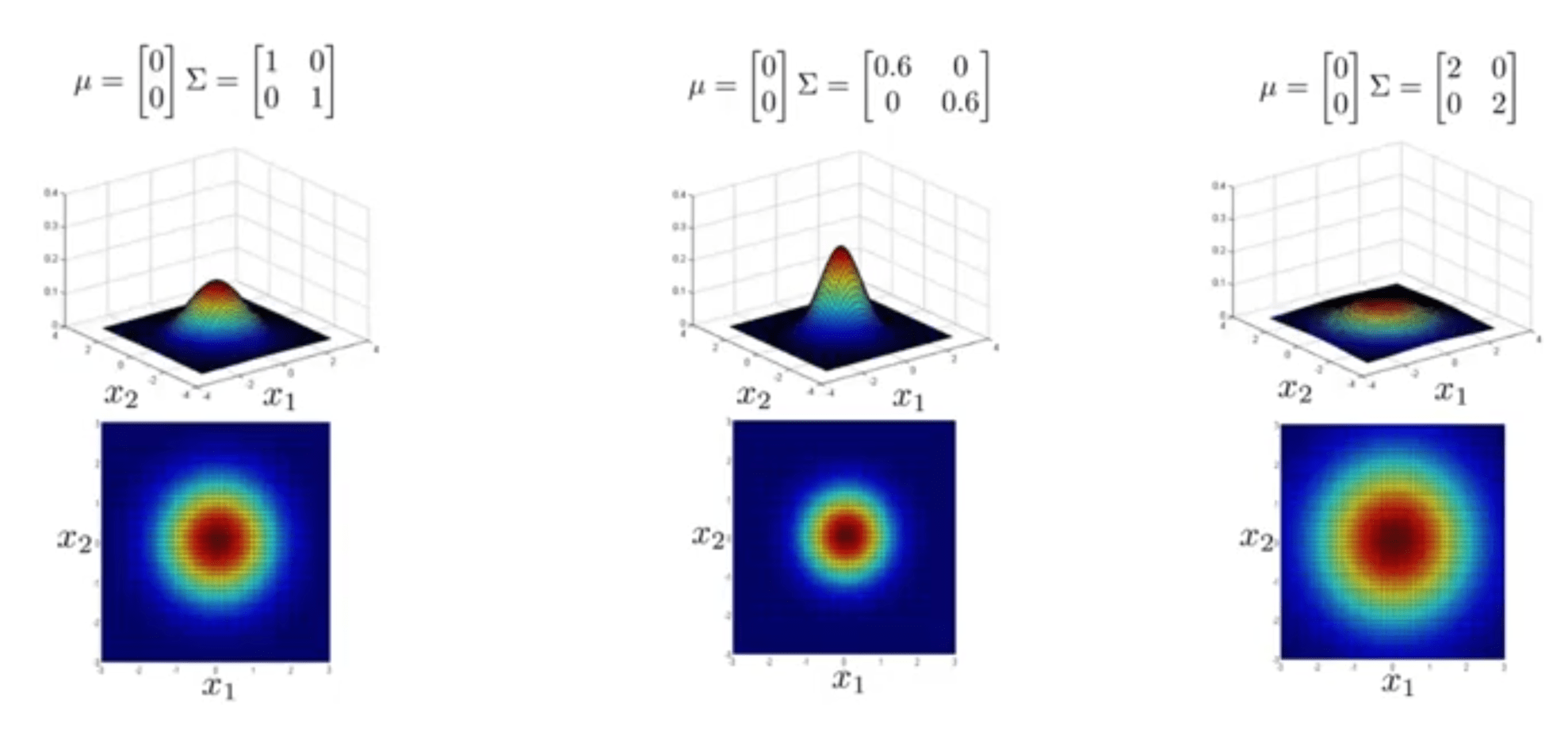
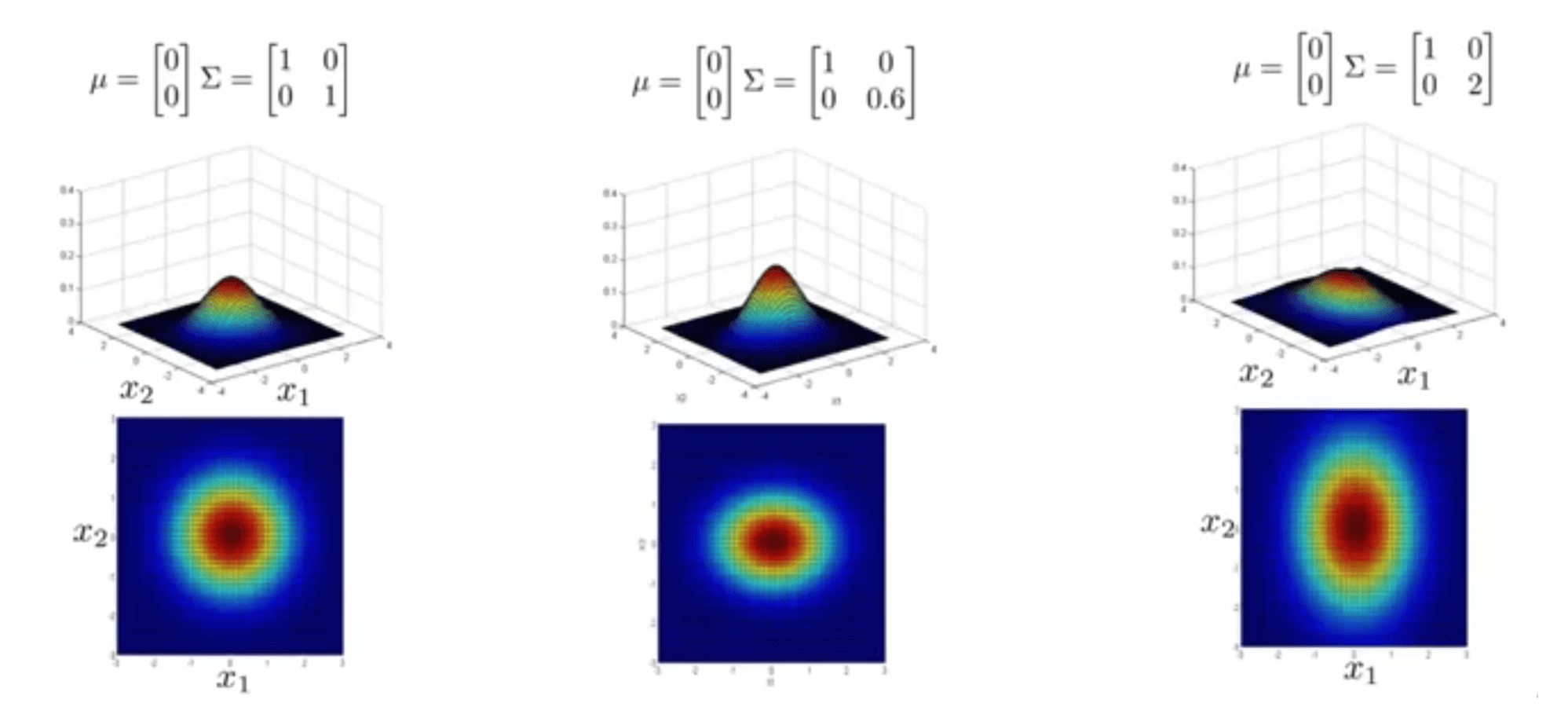
$$\begin{eqnarray} P(x;\mu,\Sigma) &=& \frac{1}{(2\pi)^{\frac{n}{2}}\det(\Sigma)^{\frac{1}{2}}} \\ &\quad& \exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)) \end{eqnarray}$$

$\det(\Sigma)$ در مخرج دترمینان ماتریس کوواریانس است. در زیر چند نمونه از مثال‌های توزیع نرمال چند متغیره نشان داده شده است.

مشاهده می‌کنید با کاهش $\Sigma$ پهنای $$p(x)$$ کم و ارتفاع آن زیاد می‌شود. همچنین برعکس با افزایش $\Sigma$ پهنای $$p(x)$$ افزایش و ارتفاع آن کم می‌شود. در شکل سمت راست هرچند تشخیص آن کمی دشوار است، ولی همان نمودار زنگوله‌ای شکل است که پهنای زیادی دارد. هر سه مورد رسم شده برای دو خصوصیت $$x_1$$ و $$x_2$$ به شکل دایره هستند که در مرکز بیشترین احتمال و هر چه از مرکز دور شویم احتمال کمتر می‌شود.

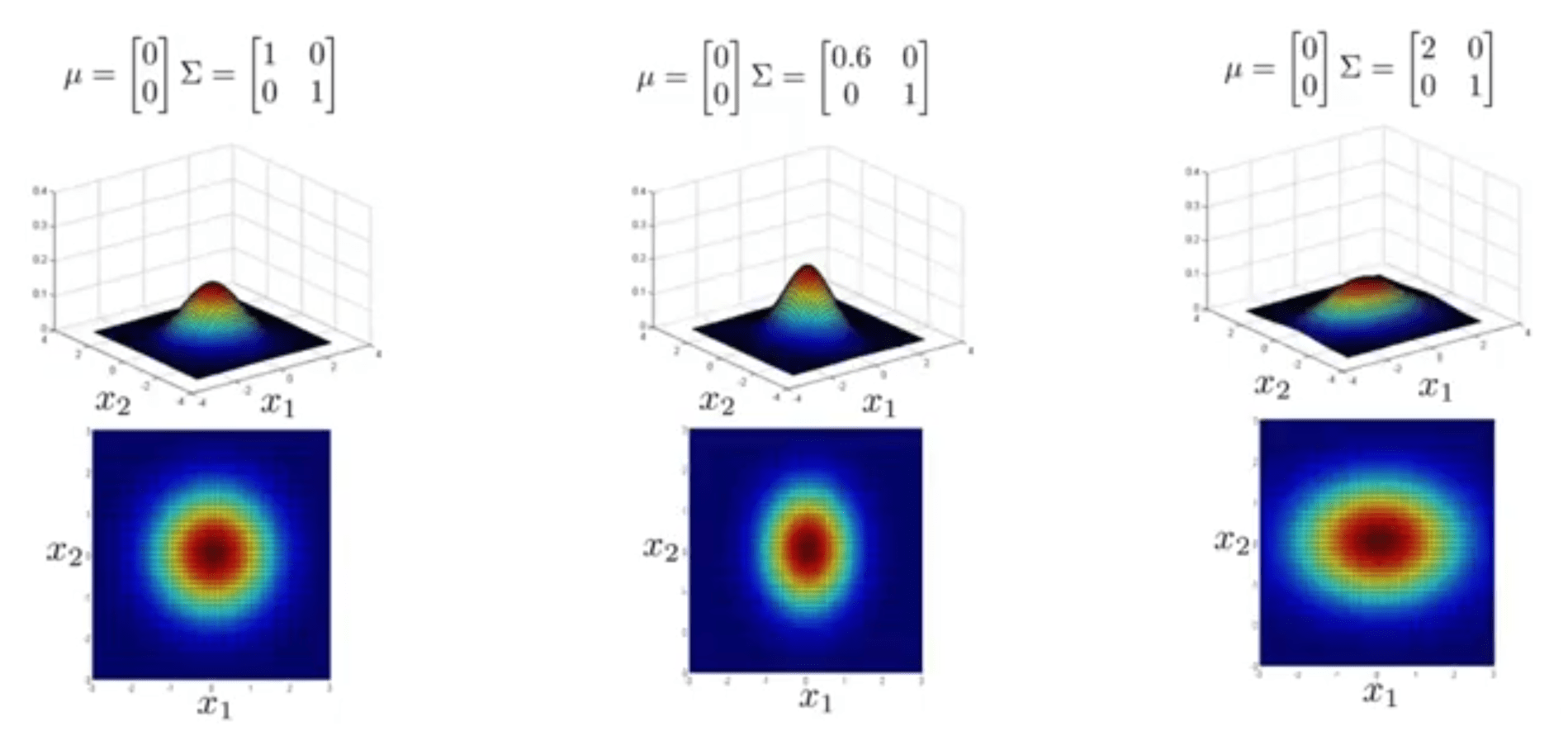
حال به مثال‌های دیگری توجه کنید.

در این مثال‌ها تنها یکی از خصوصیات را تغییر داده‌ایم. به عنوان نمونه در شکل وسط تغییرات $$x_2$$ را حفظ کرده‌ایم ولی تغییرات $$x_1$$ را کاهش داده‌ایم و در شکل سمت راست تغییرات $$x_1$$ بسیار بیشتر از $$x_2$$ است و در کنتورهای رسم شده برای $$x_1$$ و $$x_2$$ هم به وضوح این مطلب در هر دو مورد دیده می‌شود. می‌توانید مشاهده کنید که کنتورها از دایره‌ای شکل به بیضی شکل تغییر می‌کنند و تغییرات در یکی از دو راستای $$x_1$$ یا $$x_2$$ بیشتر است.

در مثال‌های زیر هم همین مطلب تکرار شده، با این تفاوت که این بار تغییرات $$x_2$$ را دستکاری کرده‌ایم.

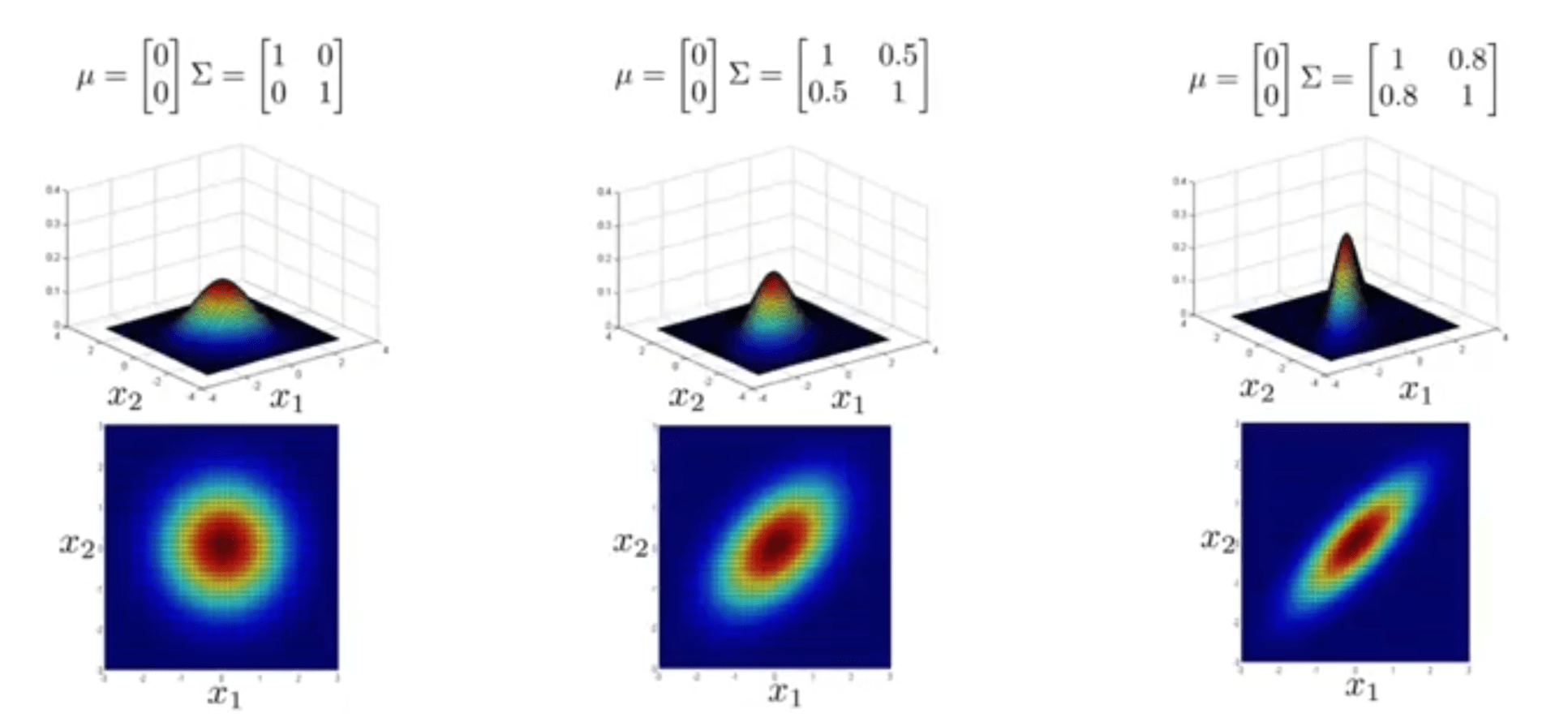
یکی از خصوصیات جالب توزیع گاوسین چند متغیره این است که می‌توان با استفاده از آن ارتباط (correlation) بین متغیرها را هم مدل کنید. به عنوان نمونه به مثال‌های زیر نگاه کنید:

در این مثال‌ها مشاهده می‌کنید با تغییر عناصر غیر قطری، کنتورهای رسم شده برای $$x_1$$ و $$x_2$$ به گونه‌ای است که نشان می‌دهد با افزایش $$x_1$$ متغیر $$x_2$$ هم افزایش پیدا می‌کند (یعنی ارتباط تنگاتنگی با هم دارند). در شکل سمت راست با افزایش مقدار عناصر غیر قطری مشاهده می‌کنید پهنای کنتورها کم شده و نمودار توزیع گاوسین $$p(x)$$ بلندتر و باریک‌تر می‌شود.

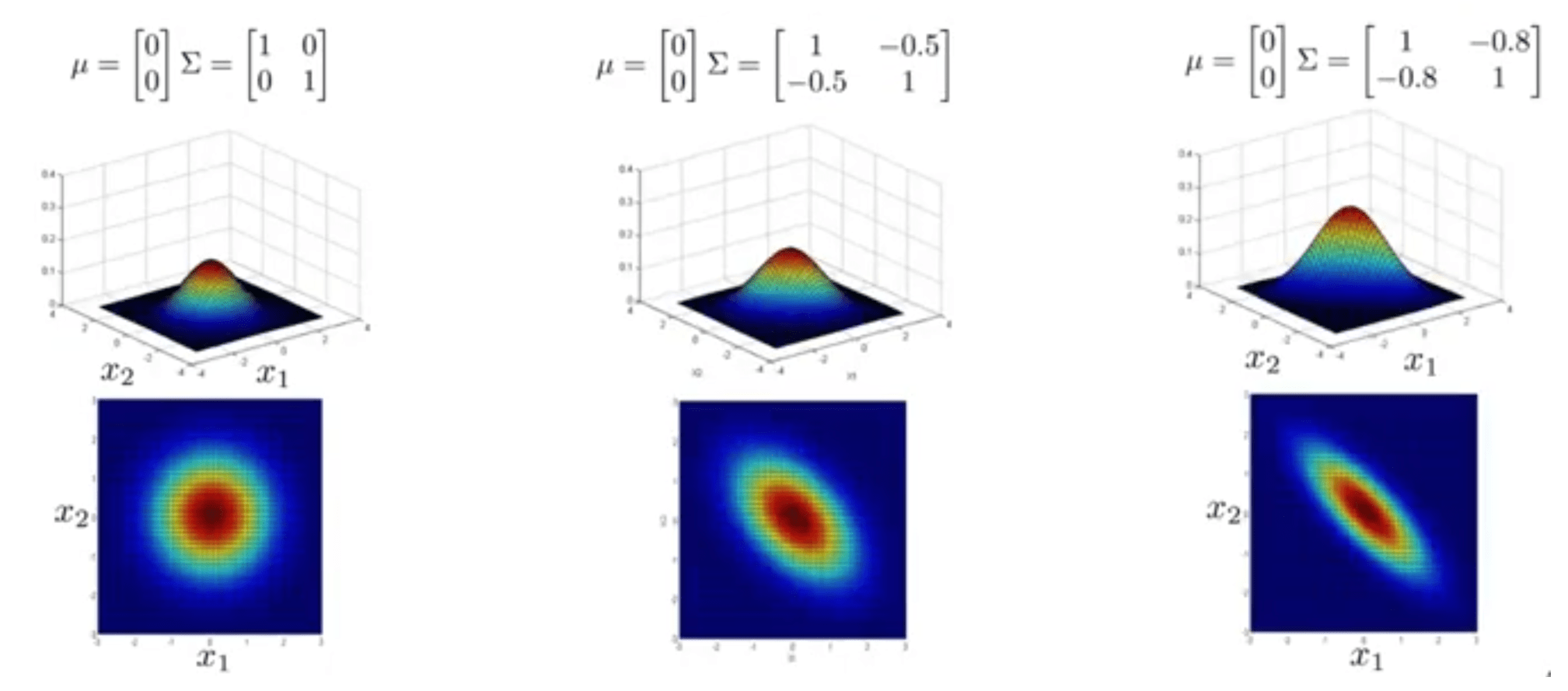
در شکل‌های زیر هم مقادیر عناصر غیر قطری منفی هستند و می‌توانید تاثیر آن را مشاهده کنید. در حالیکه یکی از متغیرها افزایش می‌یابد، متغیر دیگر کاهش پیدا می‌کند.

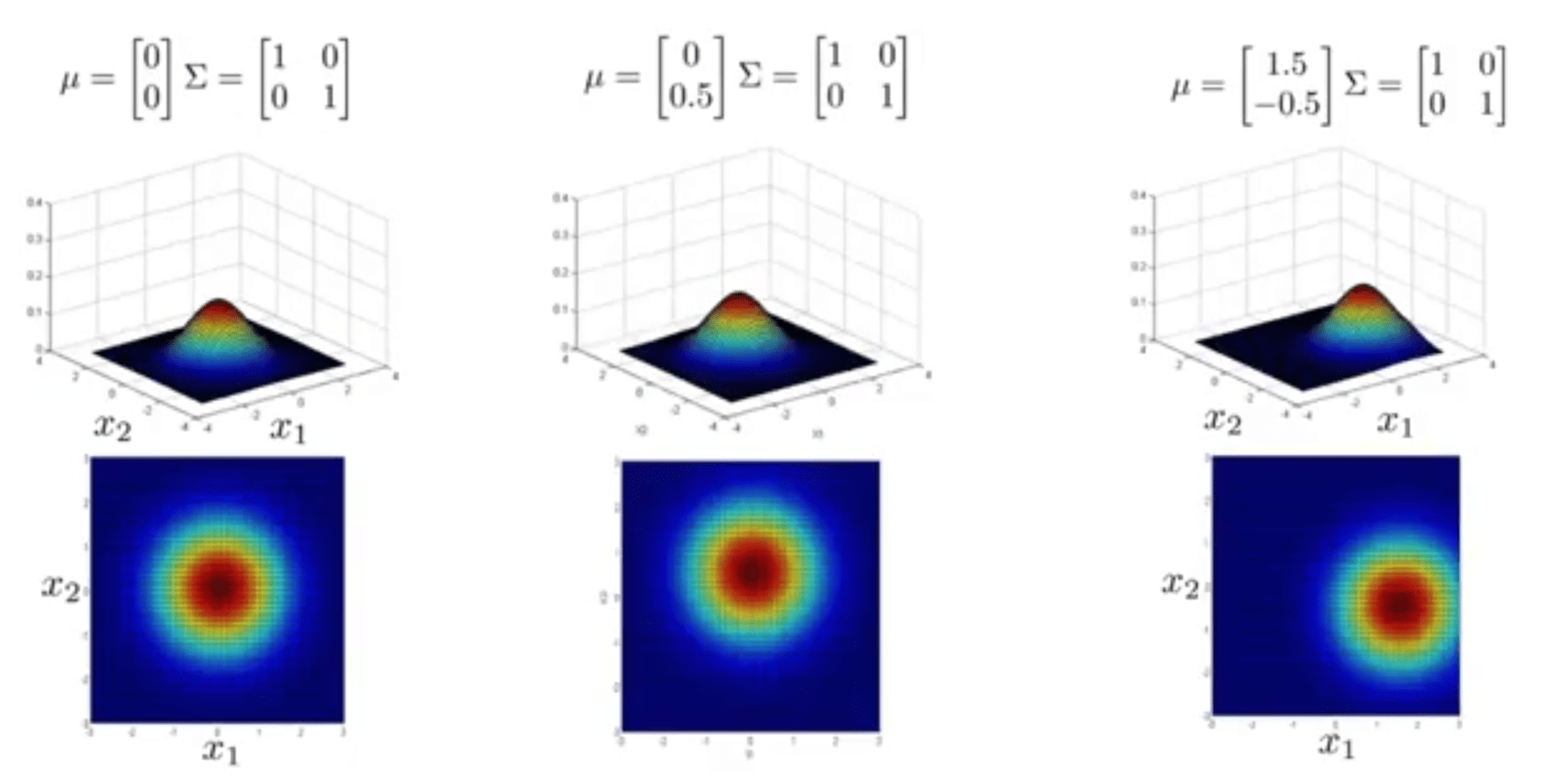
در آخر اثر تغییر مقادیر میانگین $(\mu)$ را در مثال‌های زیر مشاهده می‌کنید. به صورتی که با تغییر آن مرکز توزیع جابه‌جا می‌شود.

پس می‌توان گفت که یکی از مزایای استفاده از توزیع گاوسین چند متغیره این است که می‌تواند تغییرات خصوصیات‌هایی را که با هم در ارتباط هستند را به خوبی به نمایش بکشد و راه حلی برای مشکلی که در ابتدای این بخش مطرح شد ارائه دهد.

یافتن بی‌هنجاری با استفاده از توزیع نرمال چند متغیره

هدف ما در این بخش ارائه الگوریتمی جدید برای یافتن بی‌هنجاری بر اساس مطالب ارائه شده در قسمت قبل است. فرمول توزیع گاوسین چند متغیره را به صورت زیر نوشتیم:

$$\begin{eqnarray} P(x;\mu,\Sigma) &=& \frac{1}{(2\pi)^{\frac{n}{2}}\det(\Sigma)^{\frac{1}{2}}} \\ &\quad& \exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)) \end{eqnarray}$$

که در آن:

$$\mu = \frac{1}{m} \sum^{m}_{i=1} x^{(i)}$$

$$\Sigma = \frac{1}{m} \sum_{i=1}^{n} (x^{(i)} - \mu) (x^{(i)} - \mu)^T$$

الگوریتم:

برازش مدل $$p(x)$$ بر اساس پارامترهای $\mu$ و $\Sigma$ به مجموعه داده‌های داده شده.
محاسبه مقدار احتمالاتی برای نمونه جدید $$x$$ با استفاده از فرمول زیر
$$\begin{eqnarray} P(x;\mu,\Sigma) &=& \frac{1}{(2\pi)^{\frac{n}{2}}\det(\Sigma)^{\frac{1}{2}}} \\ &\quad& \exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)) \end{eqnarray}$$
اگر $p(x) \lt \epsilon$ آن را به عنوان نمونه بی‌هنجار شناسایی می‌کنیم.

در شکل زیر نحوه عملکرد توزیع گاوسین چند متغیره (الگوریتم معرفی شده) نشان داده شده است. چنانکه ملاحظه می‌کنید، نقطه سبز رنگ مشخص شده به درستی به عنوان نمونه بی‌هنجار شناسایی می‌شود.

ارتباط مدل گاوسین چند متغیره با مدل اصلی

اگر به خاطر داشته باشید، فرمول مدل اصلی (توزیع گاوسین تک متغیره) به شکل زیر بود:

$$ p(x) = p(x_1;\mu_1,\sigma^{2}_{2}) p(x_2;\mu_2,\sigma^{2}_{2})... p(x_n;\mu_n,\sigma^{2}_{n}) $$

چنانکه از روی شکل‌های زیر نیز مشخص است، همین شکل‌ها را برای توزیع گاوسین چند متغیره هم داشتیم. اما آنچه که اینجا وجود ندارد شکل‌هایی است که در آن محور کنتورها با محورهای $$x_1$$ و $$x_2$$ موازی نبودند.

به لحاظ ریاضی هم می‌توان ثابت کرد که مدل اصلی حالت خاصی از مدل توزیع گاوسین چند متغیره است. حالتی که در آن عناصر غیر قطری ماتریس $\Sigma$ صفر باشند و یا به عبارت دیگر:

$$ \Sigma = \begin{bmatrix} \sigma^{2}_{1} & 0 & \dots & 0 \\ 0 & \sigma^{2}_{2} & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & \sigma^{2}_{n} \end{bmatrix} $$

حال این سوال پیش می‌آید که از هر کدام در چه مواردی استفاده کنیم؟

مدل اصلی	مدل گاوسین چند متغیره
در حالتی که $$x_1$$ و $$x_2$$ ترکیبات غیرمعمولی به خود می‌گیرند، به صورت دستی خصوصیتی را جهت شناسایی بی‌هنجاری معرفی می‌کنیم. مانند مسئله بارگذاری CPU و استفاده از حافظه.	به صورت خودکار ارتباط بین خصوصیت‌ها را شناسایی می‌کند.
به لحاظ محاسباتی ارزان‌تر است. به عبارت دیگر برای $$n$$ های بزرگ راحت‌تر مقیاس می‌شود.	به لحاظ محاسباتی گران‌تر است. مثلا محاسبه معکوس $\Sigma$ را برای $$n=100000$$ در نظر بگیرید که به لحاظ محاسباتی چه هزینه‌ای را تحمیل می‌کند.
حتی اگر $$m$$ کوچک باشد الگوریتم به خوبی جواب می‌دهد.	حتما باید $m \gt n$ باشد. در غیر اینصورت $\Sigma$ معکوس‌پذیر نخواهد بود. (به عنوان یک قاعده سرانگشتی، هنگامیکه $m \gt 10n$ از آن استفاده کنید).

مشاهده می‌کنید که الگوریتم اصلی بیشتر استفاده می‌شود. تنها زمانی که می‌خواهید ارتباط بین متغیرها را به صورت خودکار شناسایی کنید (در حالتی که $$n$$ خیلی بزرگ نباشد) سراغ توزیع گاوسین چند متغیره بروید و از وقت گذاشتن برای طراحی یک خصوصیت جدید پرهیز کنید.

<< مبحث قبلی مبحث بعدی >>

مدل اصلی	مدل گاوسین چند متغیره
در حالتی که $\(x_1\)$ و $\(x_2\)$ ترکیبات غیرمعمولی به خود می‌گیرند، به صورت دستی خصوصیتی را جهت شناسایی بی‌هنجاری معرفی می‌کنیم. مانند مسئله بارگذاری CPU و استفاده از حافظه.	به صورت خودکار ارتباط بین خصوصیت‌ها را شناسایی می‌کند.
به لحاظ محاسباتی ارزان‌تر است. به عبارت دیگر برای $\(n\)$ های بزرگ راحت‌تر مقیاس می‌شود.	به لحاظ محاسباتی گران‌تر است. مثلا محاسبه معکوس $\Sigma$ را برای $\(n=100000\)$ در نظر بگیرید که به لحاظ محاسباتی چه هزینه‌ای را تحمیل می‌کند.
حتی اگر $\(m\)$ کوچک باشد الگوریتم به خوبی جواب می‌دهد.	حتما باید $m \gt n$ باشد. در غیر اینصورت $\Sigma$ معکوس‌پذیر نخواهد بود. (به عنوان یک قاعده سرانگشتی، هنگامیکه $m \gt 10n$ از آن استفاده کنید).