Large Margin Classifier

طبقه‌بندی با حاشیه زیاد

بعضی اوقات الگوریتم SVM را Large Margin Classifier به معنی طبقه‌بندی با حاشیه زیاد، می‌گویند. در این بخش دلیل این نامگذاری را توضیح خواهیم داد و این مطلب به ما کمک خواهد کرد تا بتوانیم شکل تابع فرضیه تولید شده توسط الگوریتم SVM را بدانیم.

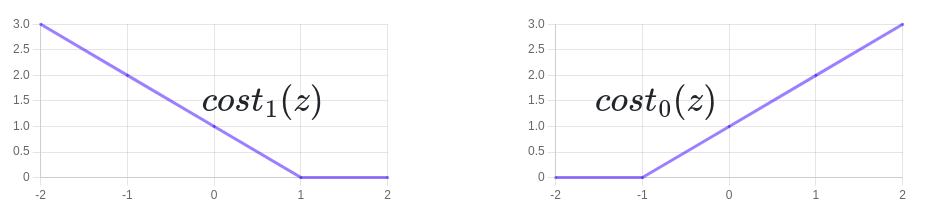
در قسمت قبل دیدیم که تابع هزینه برای الگوریتم SVM به شکل زیر است:

$$\begin{eqnarray} \min_{\theta} &C& \sum_{i = 1}^{m} \left[y^{(i)}cost_{1}(\theta^Tx^{(i)}) \right. \\ &+& \left. (1 - y^{(i)}) cost_{0}(\theta^Tx^{(i)})\right] \\ &+& \frac{1}{2} \sum_{j = 1}^{n} \theta_{j}^{2} \end{eqnarray}$$

$$ \min_{\theta} C \sum_{i = 1}^{m} \left[y^{(i)}cost_{1}(\theta^Tx^{(i)}) + (1 - y^{(i)}) cost_{0}(\theta^Tx^{(i)})\right] + \frac{1}{2} \sum_{j = 1}^{n} \theta_{j}^{2} $$

شکل سمت راست مربوط به تابع $cost_{0}(z)$ و شکل سمت چپ مربوط به تابع $cost_{1}(z)$ است.

اگر بخواهیم این تابع هزینه را کمینه کنیم، واضح است که برای حالت $$y = 1$$ می‌بایست $$z$$ یا همان $\theta^Tx$ بزرگتر از یک باشد و برای حالت $$y = 0$$ می‌بایست $$z$$ یا همان $\theta^Tx$ کوچکتر از منفی یک باشد. به عبارت ریاضی:

$$ \text{ if } y = 1, \text{ we want } \theta^Tx \ge 1 (\text{ not just } \ge 0)$$ $$ \text{if } y = 0, \text{ we want } \theta^Tx \le -1 (\text{ not just } \le 0)$$

می‌توانید مشاهده کنید که یک ضریب اطمینان بیشتری نسبت به رگرسیون لجستیک که در آن دو حالت $$y = 0$$ و $$y = 1$$ را به ترتیب با قرار دادن $\theta^Tx \lt 0$ و $\theta^Tx \ge 0$ پیش‌بینی می‌کردیم، وجود دارد.

مرز تصمیم‌گیری SVM

حالتی را در نظر بگیرید که در آن مقدار C را خیلی زیاد در نظر گرفته‌ایم مثلا $$C = 100000$$ . در این حالت جمله اول تابع هزینه باید صفر شود و در نتیجه تابع هزینه SVM به شکل زیر درخواهد آمد:

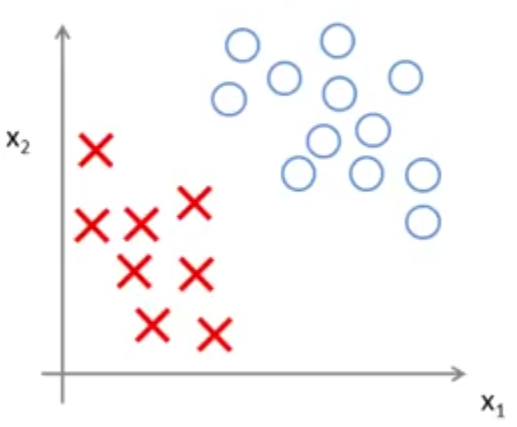
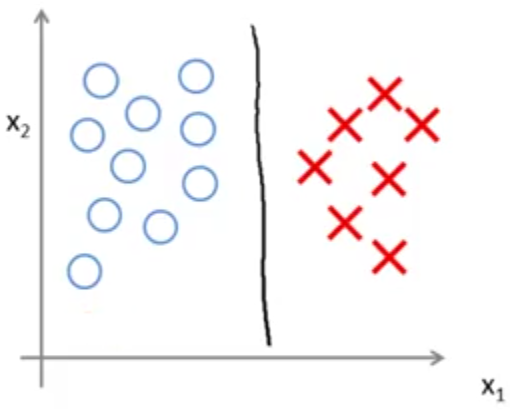
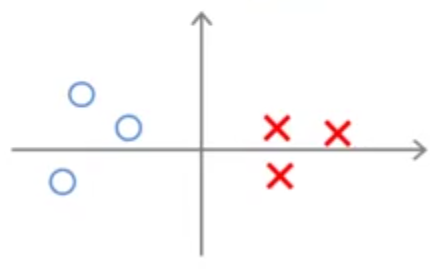
$$\begin{eqnarray} &\min_{\theta} \frac{1}{2} \sum_{j = 1}^{n} \theta_{j}^{2} \\ &s.t \quad \theta^Tx^{(i)} \ge 1 \text{ if } y^{(i)} = 1 \\ &\quad \quad \theta^Tx^{(i)} \le -1 \text{ if } y^{(i)} = 0 \\ \end{eqnarray}$$

زمانی که معادله بالا را حل کنید (کمینه کردن تابع هزینه فوق نسبت به پارامتر $\theta$ ) مرز تصمیم‌گیری (decision boundary) جالبی به ما می‌دهد. برای نمونه به داده‌های زیر نگاه کنید.

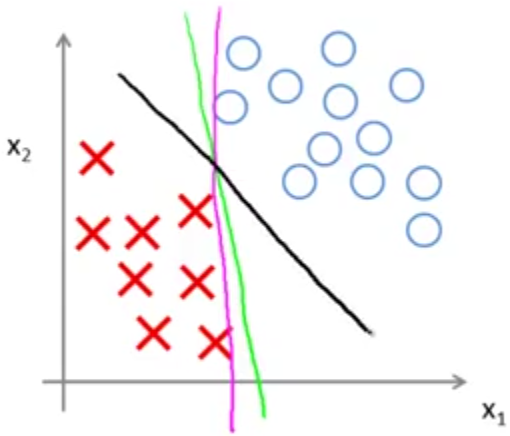
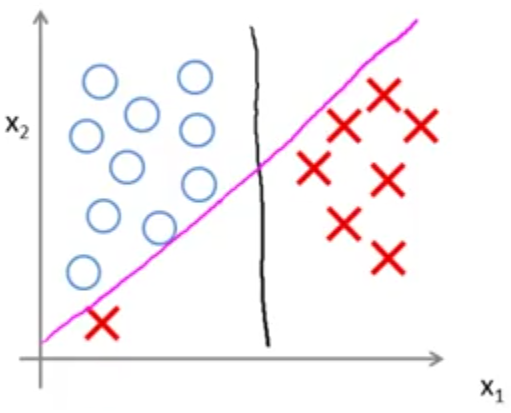
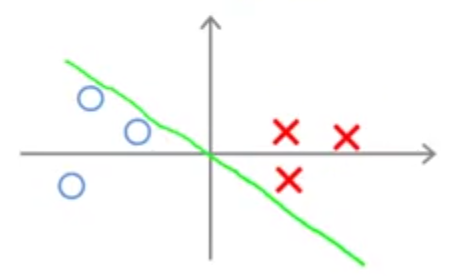
این داده‌ها به صورت خطی از هم جدا می‌شوند. به عبارت دیگر تعداد زیادی خط راست وجود دارد که می‌تواند این داده‌ها را از هم جدا کند. مانند شکل زیر:

در این میان به نظر می‌رسد بهترین خطی که داده‌ها را از هم جدا کرده، خط مشکی رنگ است. زیرا فاصله آن از هر دو نوع داده مثبت و منفی زیاد است در حالیکه دو خط دیگر بسیار نزدیک به داده‌ها، دو نوع داده را از هم جدا کرده‌اند. به فاصله خط مشکی رنگ از داده‌ها حاشیه (margin) می‌گویند و جالب اینکه با کمینه کردن تابع هزینه فوق، SVM خط مشکی رنگ را به عنوان مرز تصمیم‌گیری انتخاب می‌کند. به همین جهت به SVM طبقه‌بندی کننده با حاشیه زیاد هم گفته می‌شود.

در مورد اینکه چرا SVM سعی در انتخاب مدلی دارد که بیشتر حاشیه اطمینان را داشته باشد، در ادامه بحث خواهیم کرد ولی قبل از آن مثال دیگری که در آن داده‌های پرت وجود دارد را با هم بررسی می‌کنیم.

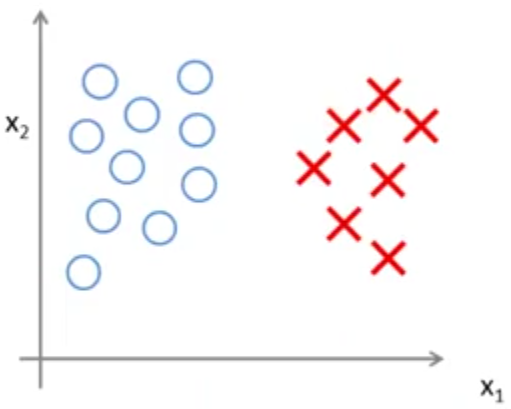
به داده‌های زیر نگاه کنید:

شاید بهترین انتخاب برای جداسازی این دو نوع داده خط مشکی رنگ رسم شده در شکل زیر باشد:

اما با انتخاب یک مقدار بسیار بزرگ برای C، در صورتیکه داده پرت وجود داشته باشد، مدل انتخابی توسط SVM ممکن است به شکل زیر تغییر کند:

در حالیکه به نظر نمی‌رسد ایده خوبی باشد تا به خاطر ضربدر قرمز رنگ گوشه نمودار مرز تصمیم‌گیری خود را عوض کنیم. ولی در صورت بزرگ بودن مقدار C الگوریتم SVM این کار را انجام خواهد داد. بنابراین بهتر است در چنین حالتی مقدار C خیلی بزرگ انتخاب نشود تا SVM بتواند کار درست را انجام دهد.

ریاضیات SVM

در این بخش می‌خواهیم به جنبه ریاضی الگوریتم SVM بپردازیم تا درک بهتری از چگونگی انتخاب مدل توسط آن داشته باشیم. این بخش اختیاری است و در صورتیکه احساس نیازی به خواندن این بخش ندارید می‌توانید به مبحث بعدی بروید.

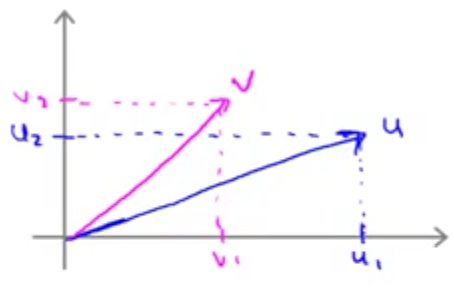
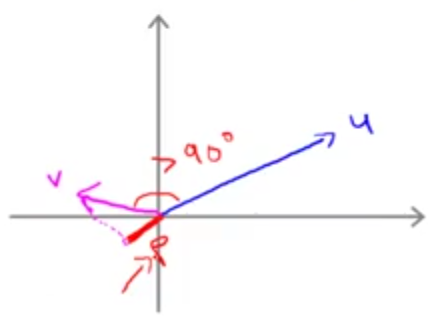
ضرب داخلی دو بردار: برای درک نحوه کارکرد الگوریتم SVM ابتدا لازم است در مورد ضرب داخلی دو بردار یادآوری داشته باشیم. فرض کنید دو بردار $u = \begin{bmatrix} u_1 \\ u_2\end{bmatrix}$ و $v = \begin{bmatrix} v_1 \\ v_2\end{bmatrix}$ را داریم که به صورت فرضی آنها را روی محورهای مختصات زیر نشان داده‌ایم.

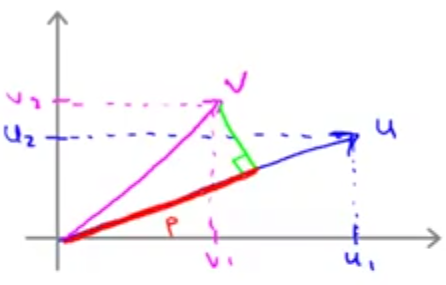
ضرب داخلی این دو بردار عبارت است از: تصویر بردار $\vec{v}$ روی بردار $\vec{u}$ (خط قرمز رنگ که با p نمایش می‌دهیم) در نرم $\vec{\lVert u \rVert}$ (طول بردار $\vec{\lVert u \rVert}$ )

$$ u^Tv = p. \lVert \vec{u} \rVert = u_1v_1 + u_2v_2 $$ $$ \lVert \vec{u} \rVert = \sqrt{u_{1}^{2} + u_{2}^{2}} \in \mathbb{R} $$

البته می‌دانیم $$u^Tv = v^Tu$$ و در نتیجه می‌توان ضرب داخلی این دو بردار را به صورت تصویر بردار $\vec{u}$ روی بردار $\vec{v}$ در نرم $\vec{\lVert v \rVert}$ هم تعریف کرد.

دقت داشته باشید که مقدار p می‌تواند منفی باشد. در حقیقت هرگاه زاویه بین دو بردار بزرگتر از ۹۰ درجه شود، مقدار p منفی خواهید شد. مانند شکل زیر.

تابع هزینه ما عبارت بود از:

برای سادگی دو فرض را در نظر می‌گیریم که البته می‌توان نشان داد تاثیری در نتیجه ندارند و تنها برای درک راحت‌تر مطالب این دو فرض را انجام می‌دهیم. فرض اول آنکه $\theta_0=0$ و این تنها بدان معنی خواهد بود که تابع فرضیه ما از مبدا مختصات عبور خواهد کرد. فرض دیگر آن است که تنها دو خصوصیت داشته باشیم تا بتوانیم آن را به راحتی روی محورهای مختصات دو بعدی نمایش دهیم.

اگر تابع هزینه را باز کنیم (با فرض $\theta_0=0$ و داشتن دو خصوصیت) خواهیم داشت:

$$\begin{eqnarray} \frac{1}{2} \sum_{j = 1}^{2} \theta_{j}^{2} &=& \frac{1}{2} (\theta_1^2 + \theta_2^2)^2 \\ &=& \frac{1}{2} (\sqrt{\theta_1^2 + \theta_2^2})^2 = \frac{1}{2} \lVert \theta \rVert^2 \end{eqnarray}$$

حال می‌خواهیم بدانیم $\theta^Tx^{(i)}$ معادل چیست؟ در زیر یک داده را با ضربدر قرمز روی محورهای مختصات مشخص کرده‌ایم. این داده در حقیقت برداری است که از مبدا مختصات تا محل آن ادامه دارد. فرض کنیم پارامتر $\theta$ هم چیزی مانند بردار آبی رنگ رسم شده باشد.

خوب ضرب داخلی $\theta$ و $$x$$ یا همان $\theta^Tx^{(i)}$ چه خواهد بود؟ با توجه به آنچه که در بخش یاد‌اوری ضرب داخلی گفتیم، ضرب داخلی این دو برابر خواهد بود با تصویر $$x$$ روی بردار $\theta$ در اندازه بردار $\theta$ .

$$ \theta^Tx^{(i)} = p^{(i)}. \lVert \vec{\theta} \rVert = \theta_1x_1^{(i)} + \theta_2x_2^{(i)} $$

با توجه به رابطه به دست آمده می‌توانیم تابع هزینه SVM را به صورت زیر بازنویسی کنیم:

$$\begin{eqnarray} &\min_{\theta} \frac{1}{2} \sum_{j = 1}^{n} \theta_{j}^{2} = \frac{1}{2} \lVert \vec{\theta} \rVert^2 \\ &s.t \quad p^{(i)}. \lVert \theta \rVert \ge 1 \text{ if } y^{(i)} = 1 \\ &\quad \quad p^{(i)}. \lVert \theta \rVert \le -1 \text{ if } y^{(i)} = 0 \\ \end{eqnarray}$$

که در آن $p^{(i)}$ تصویر $x^{(i)}$ روی بردار $\theta$ است.

حال با توجه به مثال زیر می‌خواهیم بررسی کنیم چرا الگوریتم SVM مرز تصمیم‌گیری را با بیشترین حاشیه ممکن انتخاب می‌کند.

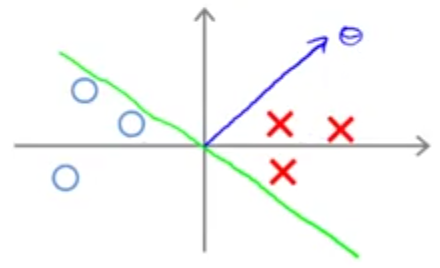
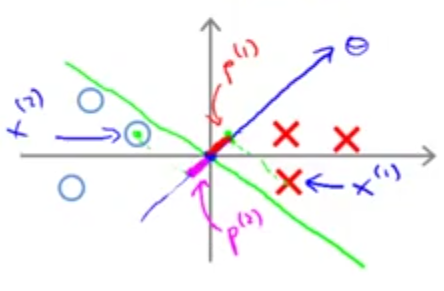
یکی از راه‌های جداسازی دو نوع داده نشان داده شده می‌تواند مانند شکل زیر باشد:

اما چرا SVM این را انتخاب نمی‌کند؟ می‌توان نشان داد که پارامتر $\theta$ بر مرز تصمیم‌گیری عمود است. بنابراین مرز تصمیم‌گیری نشان داده شده مربوط به بردار $\theta$ زیر خواهد بود.

دلیل اینکه مرز تصمیم‌گیری از مبدا مختصات عبور کرده است، در نظر گرفتن فرض ساده کننده $\theta_0 = 0$ می‌باشد. در زیر تصویر دو داده را روی بردار $\theta$ نشان داده‌ایم. چنانکه ملاحظه می‌کنید اندازه تصویر آنها کوچک است در نتیجه برای آنکه عبارت $p^{(i)}. \lVert \theta \rVert \ge 1$ یا $p^{(i)}. \lVert \theta \rVert \le 1$ برقرار باشند، مقدار $\theta$ می‌بایست بزرگ باشد در حالیکه هدف تابع هزینه ما کمینه کردن $\theta$ است.

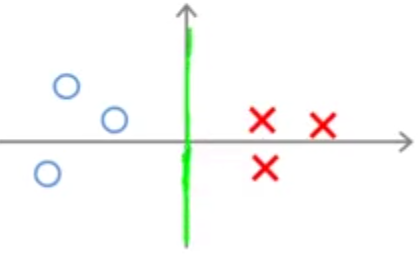
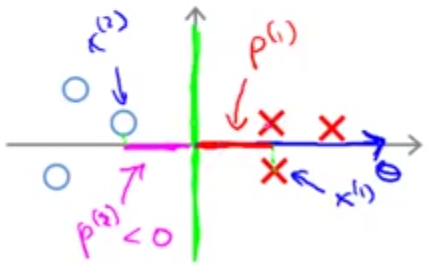
حال مرز تصمیم‌گیری زیر را در نظر بگیرید:

با رسم تصویر داده‌ها روی بردار $\theta$ مشاهده می‌کنیم نسبت به حالت قبل مقدار $p^{(i)}$ بیشتر است و در نتیجه جهت برقراری عبارت $p^{(i)}. \lVert \theta \rVert \ge 1$ یا $p^{(i)}. \lVert \theta \rVert \le 1$ مقدار $\theta$ کوچک‌تر از حالت قبل خواهد بود. به همین جهت الگوریتم SVM این مرز را انتخاب می‌کند.

<< مبحث قبلی مبحث بعدی >>