K-means Algorithm

الگوریتم K-means

در مسئله‌ی خوشه‌بندی، یک مجموعه داده بدون برچسب به ما داده شده و می‌خواهیم که الگوریتم یادگیری این داده‌ها را به صورت اتوماتیک به گروه‌هایی که یک ارتباط منطقی را بین آن‌ها برقرار می‌کند دسته‌بندی نماید. برای انجام این کار الگوریتم K-means با اختلاف زیاد محبوب‌ترین و پر استفاده ترین الگوریتم است و در این بخش می‌خواهیم درباره‌ی آن صحبت کنیم.

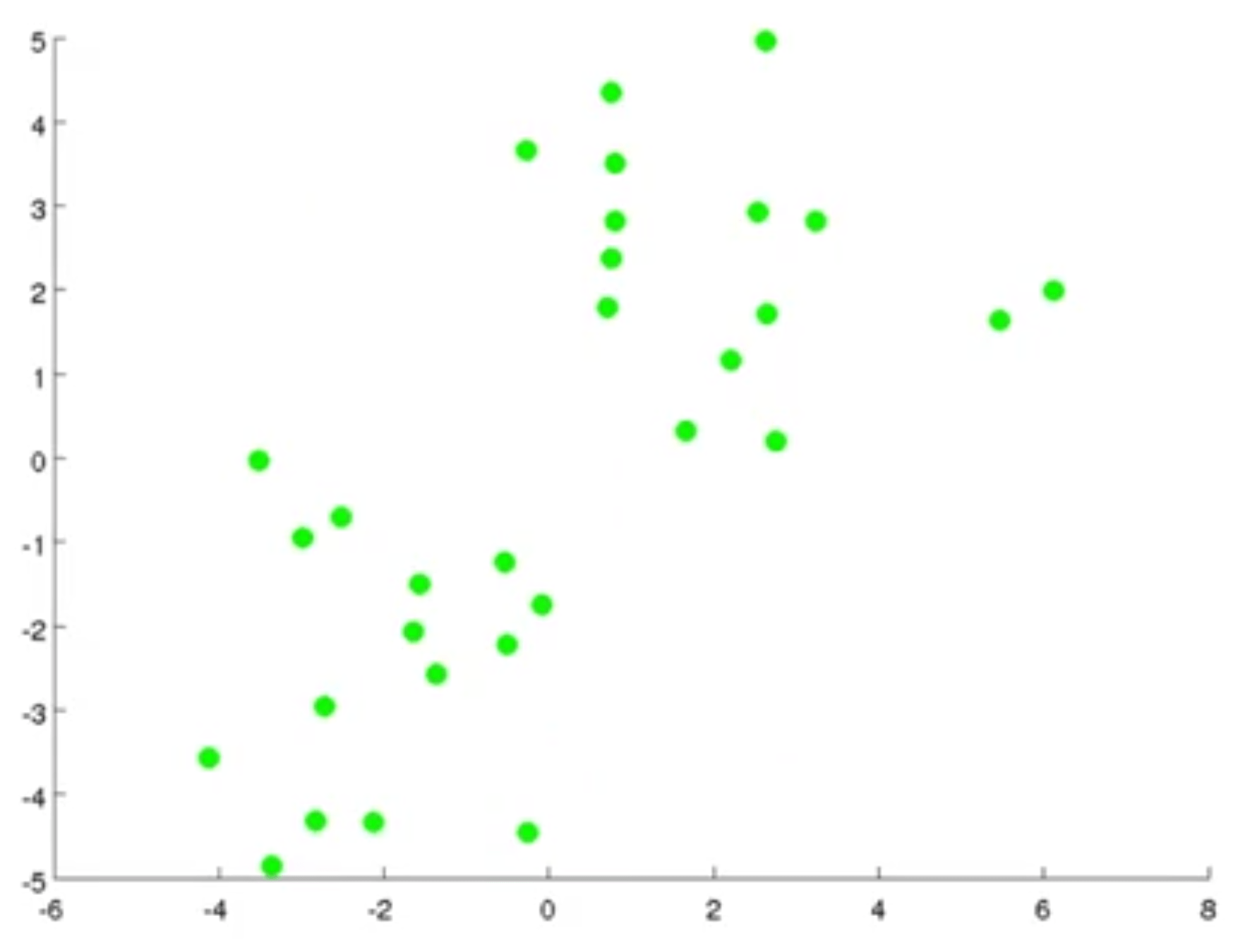
بهترین راه برای توضیح الگوریتم K-means به صورت تصویری است. فرض کنید یک مجموعه داده به شکل زیر داریم و می‌خواهیم که این داده‌ها را به 2 خوشه تقسیم کنیم.

اگر بخواهیم به‌وسیله‌ی الگوریتم K-means این کار را انجام دهیم به این شکل عمل خواهیم کرد:

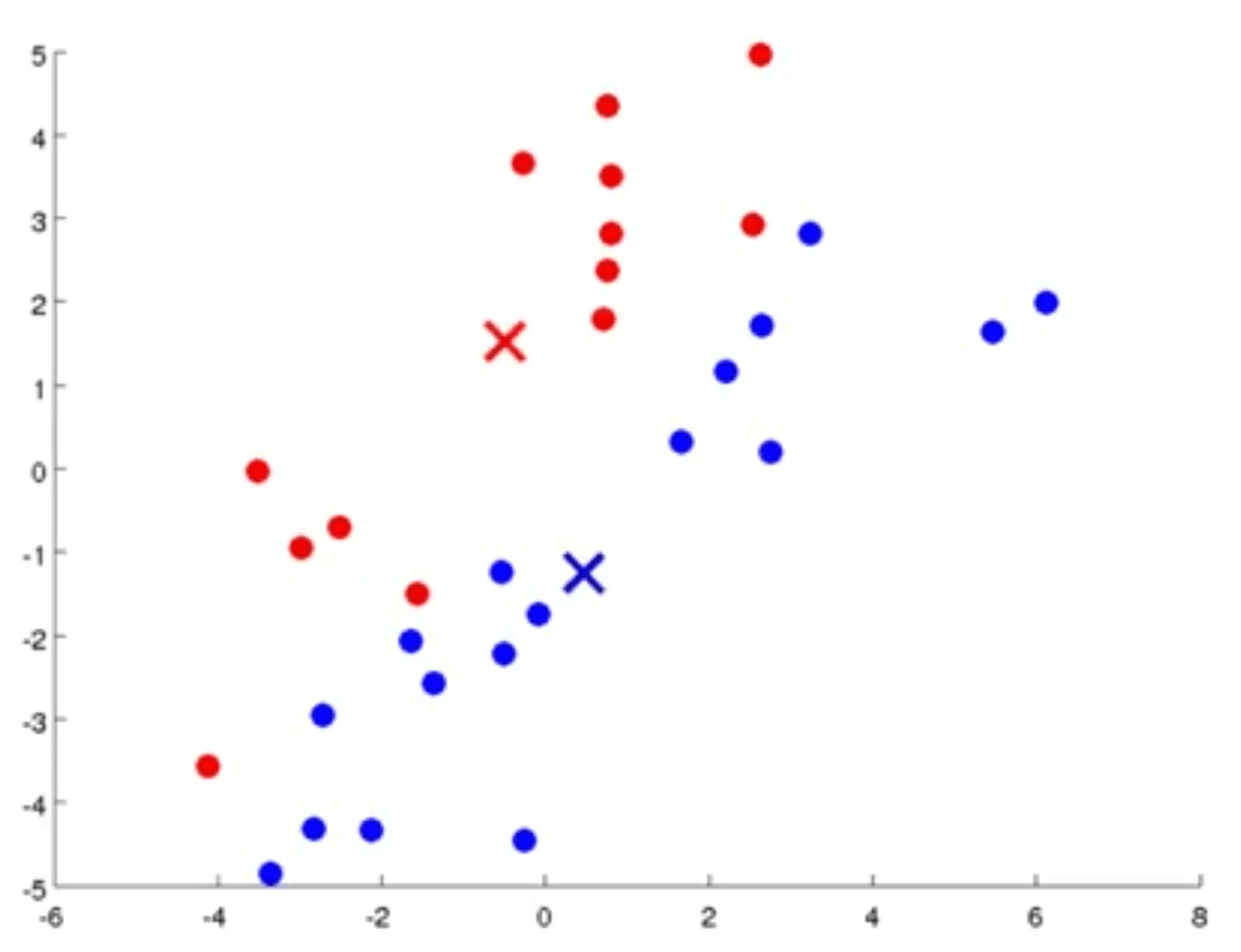
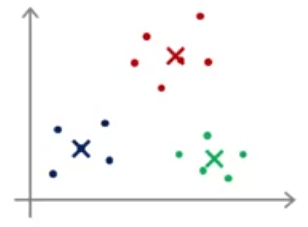
ابتدا به صورت تصادفی 2 نقطه را به عنوان مرکز خوشه‌ها مشخص می‌کنیم. (علامت‌های ضربدر آبی و قرمز در شکل زیر)

الگوریتم K-means یک الگوریتم بر اساس تکرار است و دو کار انجام می‌دهد:
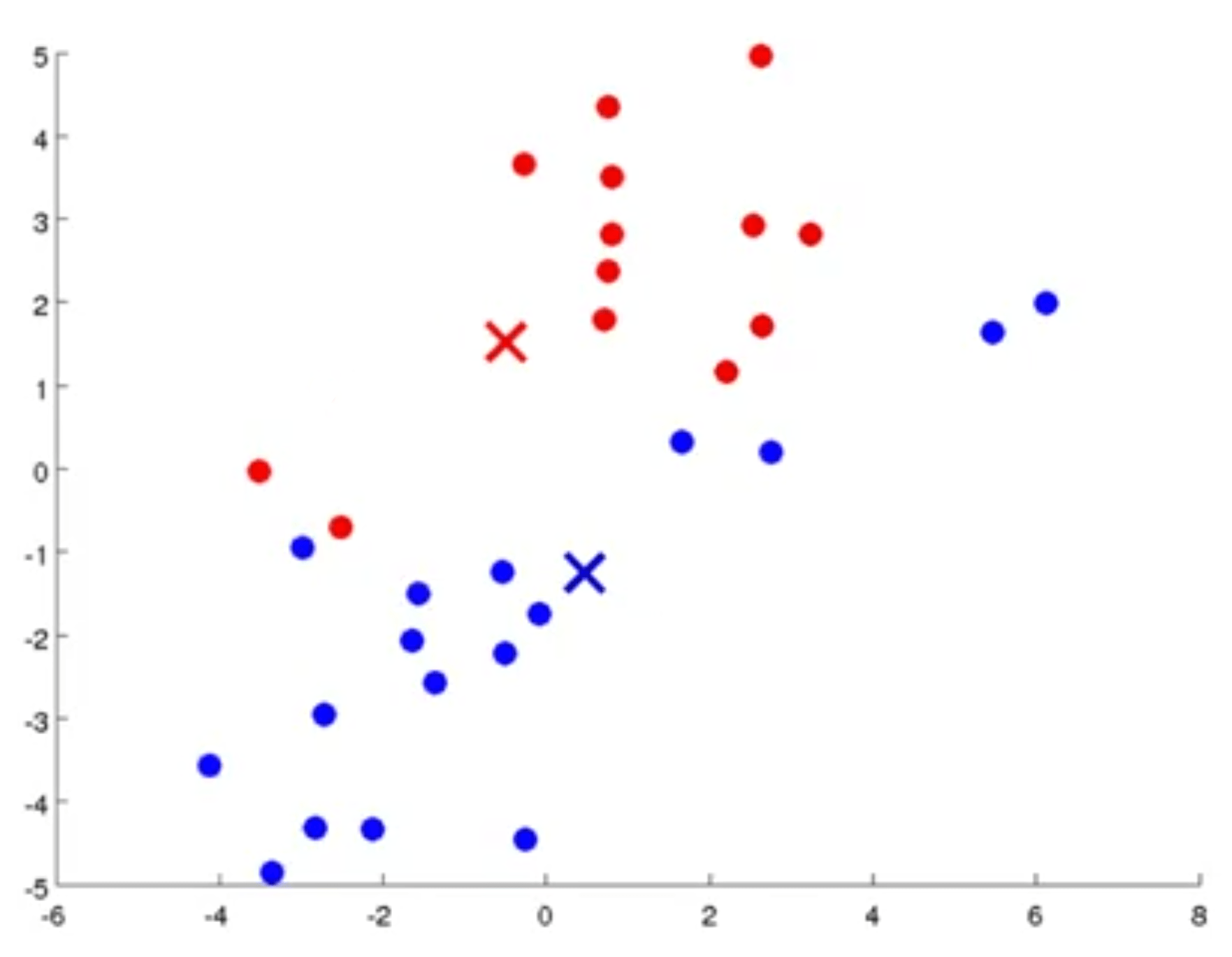
1. تخصیص خوشه: برای هر داده (نقاط سبز رنگ) مشخص می‌کند که آیا به مرکز آبی رنگ یا به مرکز قرمز رنگ نزدیک‌تر است و هر یک از داده‌ها را به یکی از این 2 مرکز تخصیص می‌دهد. مانند شکل زیر:
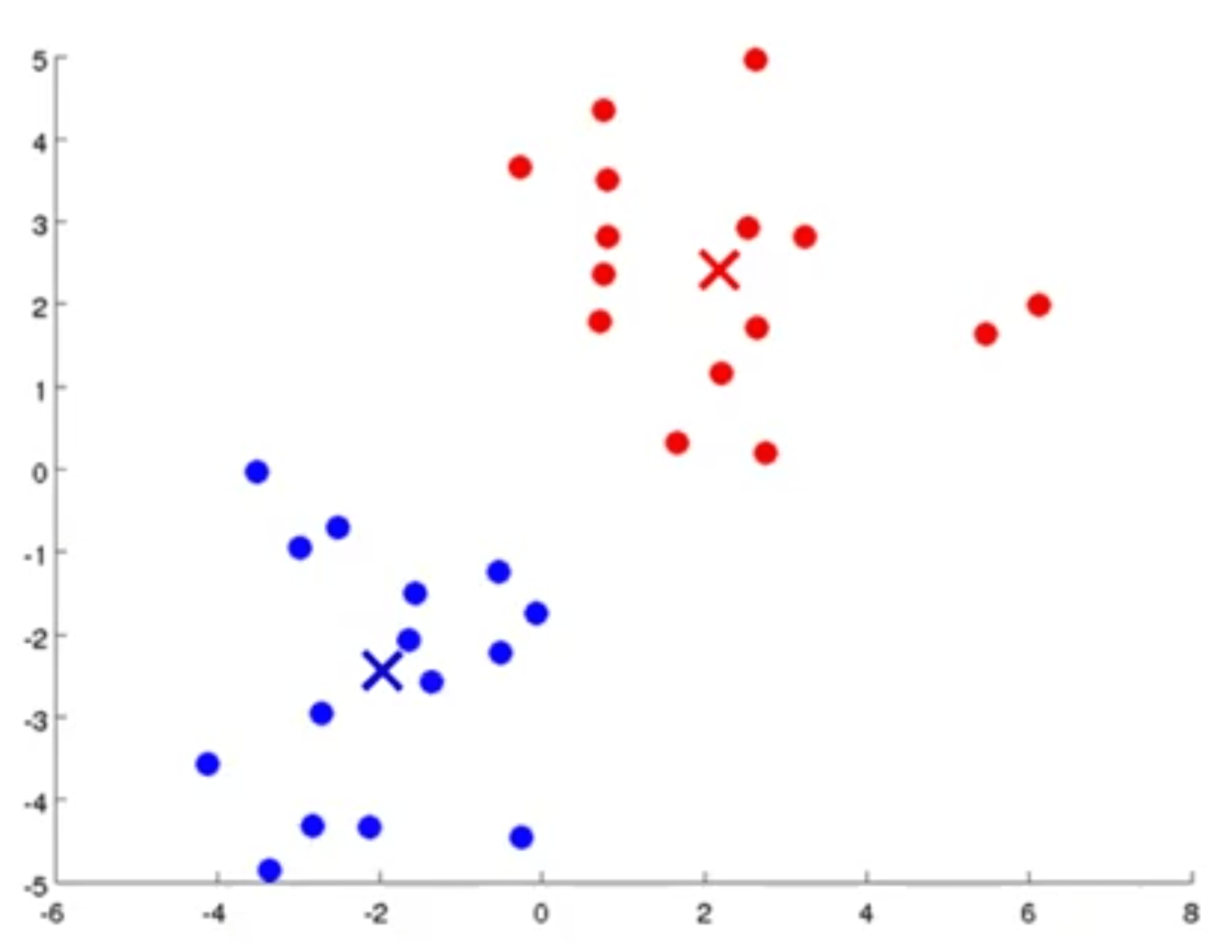
2. حرکت دادن مرکز خوشه‌ها: براساس میانگین فاصله نقاط هم‌رنگ با مرکز خوشه، مرکز خوشه حرکت داده می‌شود. مثلا درشکل زیر مکان مرکز خوشه‌ها براساس میانگین نقاط هم‌رنگ با مرکز خوشه حرکت داده شده‌اند. (نسبت عکس قبلی)

در تکرار بعد دوباره به گام اول یعنی اختصاص داده‌ها به مرکز خوشه‌ها برمی‌گردیم و دوباره براساس اینکه هر نقطه (داده) به کدام مرکز خوشه نزدیک است آن‌ها را به رنگ مرکز خوشه‌ها در می‌آوریم.

در مرحله دوم تکرار- مرکز خوشه‌ها را دوباره براساس میانگین نقاط هم‌رنگ با آن‌ حرکت می‌دهیم.

این کار را آنقدر ادامه می‌دهیم تا دیگر مرکز خوشه و رنگ داده‌ها دیگر تغییر نکند.

در این مثال بسیار خوب 2 خوشه را برای دسته‌بندی داده‌ها پیدا کرده است. اما تعریف رسمی K-means به شکل زیر است:

الگوریتم K-means به دو ورودی نیاز دارد:

K تعداد خوشه‌ها
مجموعه داده‌های آموزش $\{x^{(1)},...,x^{(m)}\}$

دقت داشته باشید که

x^{(i)} \in mathbb{R}^n

است. یعنی قرار داد

\(x_0 = 1\)

را دیگر در اینجا به کار نمی‌بریم.

الگوریتم K-means:

به صورت تصادفی K مرکز خوشه، $\mu_1,...,\mu_K \in mathbb{R}^n$ را مشخص می‌کنیم سپس:

$$\begin{eqnarray} \text{Repeat} &\quad& \{ \\ &\quad& \quad \text{for } i = 1\text{ to } m \\ &\quad& \quad \quad c^{(i)} := \text{index (from 1 to K) of} \\ &\quad& \quad \quad \quad \text{cluster centroids closest to } x^{(i)} \\ &\quad& \quad \text{for } k = 1 \text{ to } K \\ &\quad& \quad \quad \mu_k := \text{ average (means) of points} \\ &\quad& \quad \quad \quad \text{assigned to cluster k} \\ &\quad& \} \end{eqnarray}$$

$\mu$ ها در الگوریتم بالا مراکز خوشه‌ها هستند و چنانکه ملاحظه می‌کنید الگوریتم ما 2 حلقه‌ for دارد:

حلقه‌ داخلی هر نقطه از داده‌های ما را به مرکز خوشه‌ای که به آن نزدیک‌تر است اختصاص می‌دهد. که به عبارت ریاضی می‌توان گفت:

$$ \min_{k} \lVert x^{(i)} - \mu_k \rVert $$

مقدار kایی که عبارت بالا را کمینه کند، همان $c^{(i)}$ است.

حلقه‌ دوم میانگین نقاط اختصاص داده شده به خوشه kام را محاسبه و براساس آن مرکز خوشه را حرکت می‌دهد.

کاربردی از الگوریتم K-means

قبل از پایان این بخش به کاربرد دیگری از K-means اشاره می‌کنیم و آن استفاده از الگوریتم K-means برای خوشه‌هایی است که به خوبی از یکدیگر جدا نیستند. برای درک مطلب ابتدا به شکل زیر نگاه کنید:

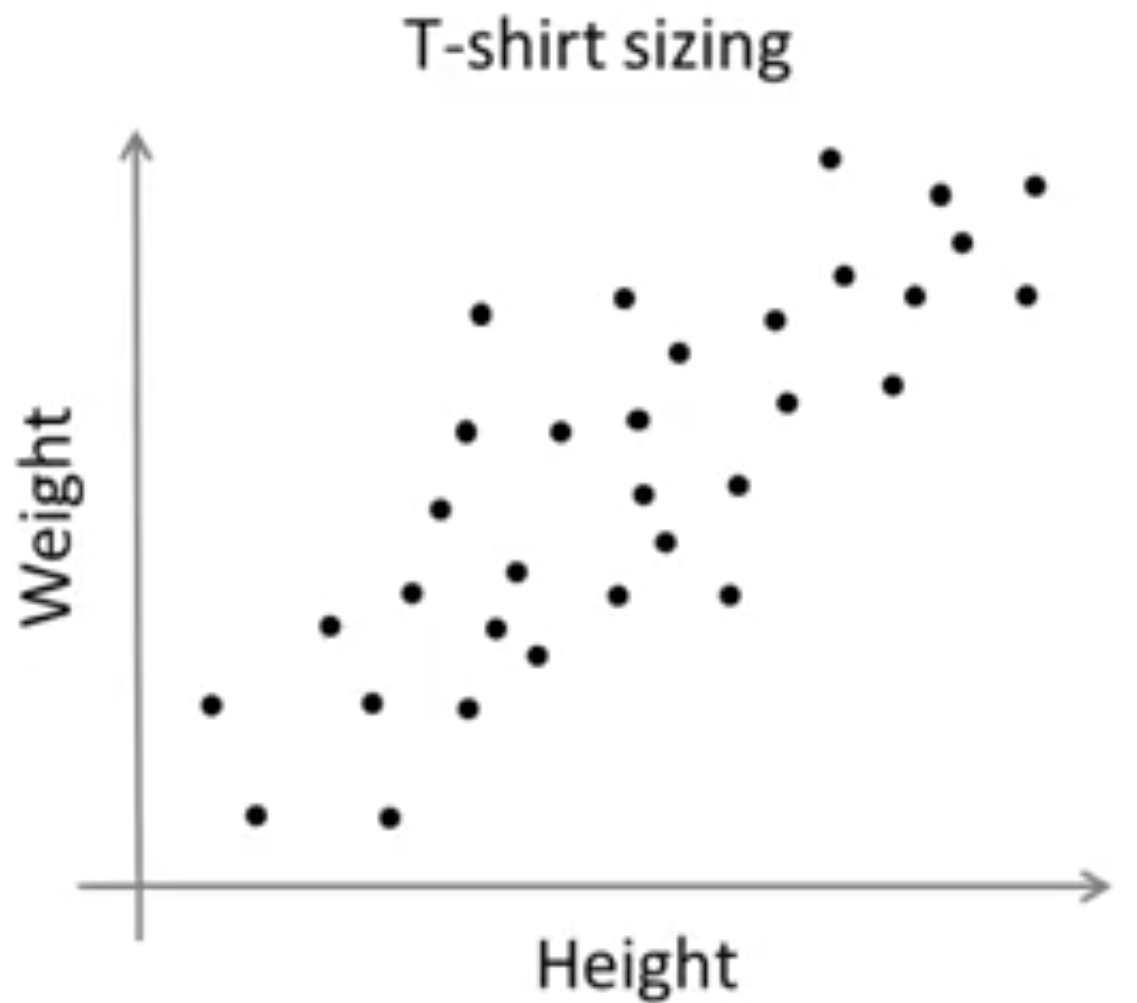
در این شکل به صورت واضح 3 خوشه متفاوت را می‌توان تشخیص داد ولی اغلب اوقات ممکن است داده‌ها به شکل زیر باشند:

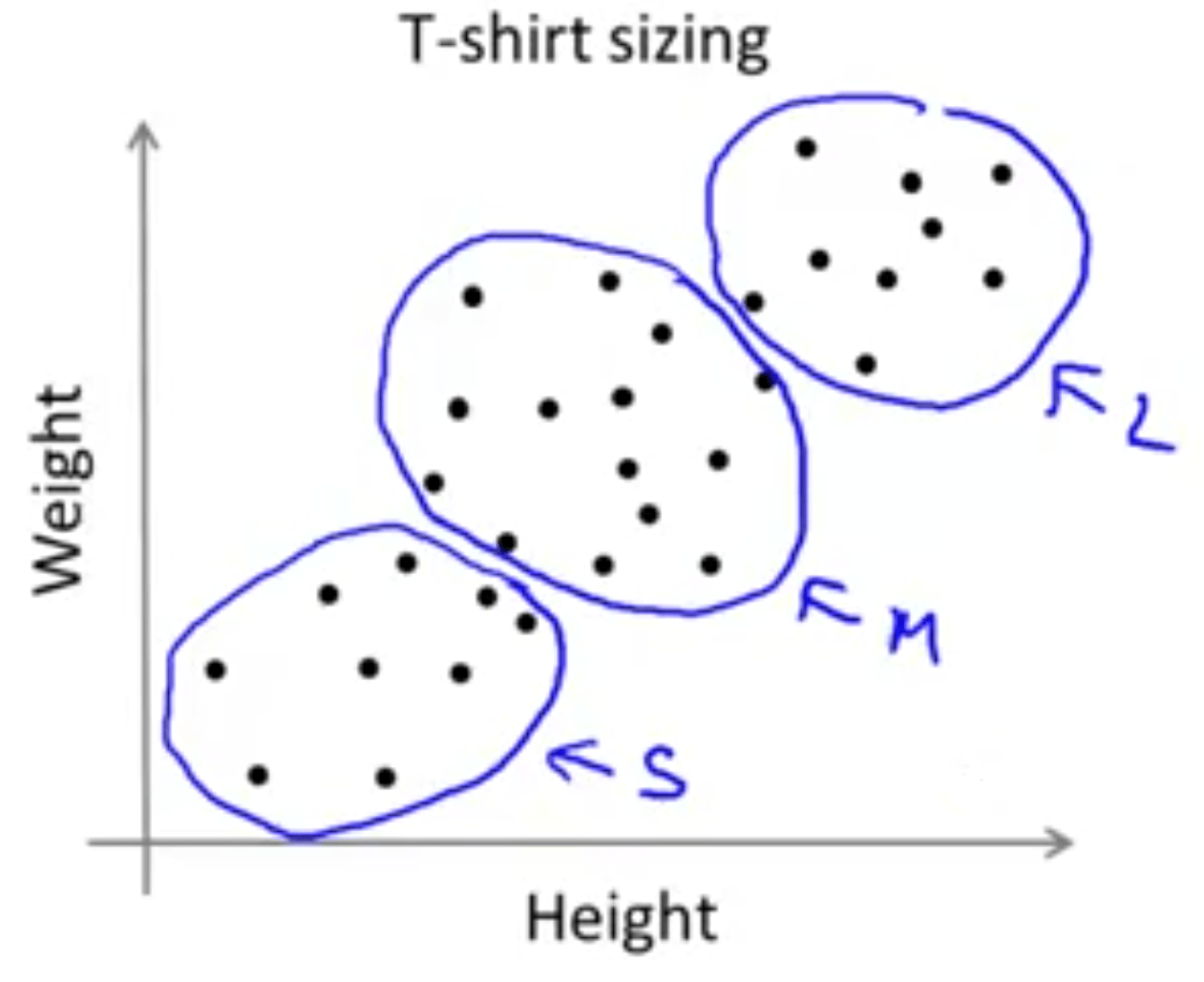
چنانکه ملاحظه می‌کنید نمی‌توان به صورت واضح تعداد خوشه‌های جدا از هم را تشخیص داد. در اینگونه موارد باید کاربرد خوشه‌بندی را مد نظر قرار داد. به عنوان مثال در شکل بالا فرض کنید که یک تولید کننده تی‌شرت تعدادی از قد و وزن مشتریان خود را جمع‌آوری کرده است. حال براساس این داده‌ها می‌خواهد اندازه تی‌شرت‌های تولیدی خود را مشخص کند. مثلا در 3 سایز مختلف تی‌شرت‌هارا تولید کند. کوچک (S)، متوسط (M) و بزرگ (L). سوال این است که از هر کدام چقدر تولید شود؟ یکی از راه‌های پاسخ به این سوال اجرای K-means با تعداد 3 خوشه است. در این حالت ممکن است الگوریتم K-means شکل زیر را برای ما فراهم کند:

بنابراین مشاهده می‌کنید داده‌هایی که در ابتدا به نظر نمی‌رسید به خوشه‌هایی متفاوتی تقسیم شوند توسط الگوریتم K-means و براساس نیاز به 3 خوشه تقسیم شدند.

تابع هزینه

در همه‌ الگوریتم‌هایی که در یادگیری با نظارت بررسی کردیم، یک تابع هزینه داشتیم که الگوریتم سعی در کمینه کردن آن داشت. الگوریتم K-means یک هدف بهینه سازی (Optimization Objective) یا همان تابع هزینه دارد و سعی در کمینه کردن آن دارد.

در این بخش می‌خواهیم این تابع هزینه را معرفی کنیم. این معرفی به 2 دلیل برای ما مفید خواهد بود: اول آنکه دانستن تابع هزینه K-means زدایی به ما در باگ‌ (debugging) الگوریتم کمک خواهد کرد و دلیل دوم و مهم‌تر آنکه می‌توانیم در پیدا کردن خوشه‌بندی بهتر توسط K-means تصمیم‌گیری کنیم.

تابع هزینه الگوریتم K-means:

$$\begin{eqnarray} J(c^{(1)},&.&..,c^{(m)},\mu_1,...,\mu_k) = \\ &\frac{1}{m}& \sum_{i=1}^{m} \lVert x^{(i)} - \mu_{c^{(i)}} \rVert \end{eqnarray}$$ $$ \min_{\substack{c^{(1)},...,c^{(m)} \\ \mu_1,...,\mu_k}} J(c^{(1)},...,c^{(m)},\mu_1,...,\mu_k) $$

اگر نگاهی دوباره به الگوریتم K-means بیاندازیم:

مشاهده می‌کنیم که این الگوریتم در حلقه اول تابع هزینه نوشته شده در بالا را نسبت به پارامتراهای $c^{(1)},...,c^{(m)}$ با ثابت نگه داشتن مرکز خوشه‌ها کمینه می‌کند و حلقه دوم تابع هزینه را نسبت به مرکز خوشه‌ها یعنی پارامتراهای $\mu_1,...,\mu_k$ کمینه می‌کند.

حالا که می‌دانیم که چه تابع هزینه‌ای را کمینه می‌کنیم می‌توانیم الگوریتم K-means را باگ زدایی کنیم و مطمئن شویم که تابع هزینه همگرا می‌شود.

مقداردهی اولیه به صورت تصادفی

در این بخش بحث را با نحوه‌ مقداردهی اولیه به صورت تصادفی برای الگوریتم K-means آغاز می‌کنیم. این بحث نهایتا منجر به بحث مهم درباره چگونگی اجتناب K-means در پیدا کردن نقاط کمینه‌ محلی (چگونه خوشه‌بندی بهتری را پیدا کنیم) می‌شود..

تا به اینجا در مورد اولین گام الگوریتم K-means یعنی مقداردهی اولیه مرکز خوشه‌ها به صورت تصادفی بحثی نکرده‌ایم. برای این‌کار راه‌های بسیار متفاوتی وجود دارد ولی یکی از این روش‌ها بیشتر از سایر روش‌های دیگر توصیه می‌شود. برای توضیح این روش‌ها در نظر داشته باشید که در هنگام اجرای الگوریتم K-means می‌بایست تعداد خوشه‌ها از تعداد نقاط داده‌های ما کمتر باشد یعنی $K \lt m$ .

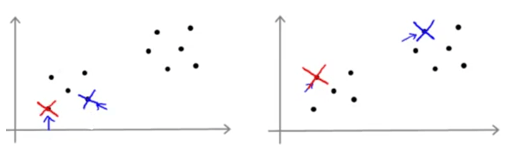
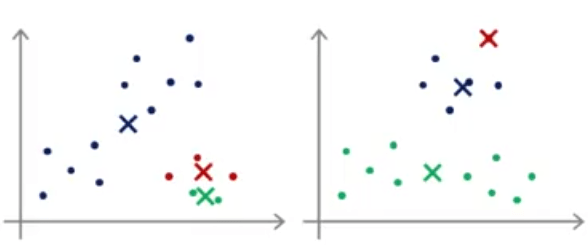
با در نظر گرفتن این نکته، معمولا برای انتخاب مرکز خوشه‌ها، به صورت تصادفی $$K$$ نمونه از داده‌ها را انتخاب می‌کنیم و $\mu_1$ تا $\mu_K$ را برابر این $$K$$ نمونه قرار می‌دهیم. به عنوان مثال به دو شکل زیر دقت کنید:

با انتخاب تصادفی از داده‌ها به عنوان مرکز خوشه، مشاهده می‌کنید که در شکل سمت راست نسبت به سمت چپ خوش‌شانس‌تر بوده‌ایم. با توجه به این 2 شکل می‌توان حدس زد که بسته به نحوه‌ مقداردهی اولیه ممکن است الگوریتم K-means به پاسخ‌های متفاوتی برسد. به عنوان مثال فرض کنید داده‌هایی به شکل زیر داریم:

هرچند در این داده‌ها به وضوح 3 خوشه دیده می‌شود و در صورت اجرای درست الگوریتم K-means می‌توانیم مانند شکل زیر به نقاط کمینه‌ سراسری برسیم:

ولی اگر مقداردهی اولیه‌ شما با بدشانسی همراه باشد احتمال دارد که الگوریتم به کمینه‌های محلی برسد و خوشه‌هایی به شکل زیر ایجاد شوند:

بنابراین اگر نگران این هستید که الگوریتم K-means در کمینه‌های محلی گیر کند و می‌خواهید احتمال پیدا کردن بهترین خوشه‌های ممکن توسط الگوریتم K-means را بالا ببرید، می‌توانید به‌ جای اجرای یکبار الگوریتم و امید به اینکه بهترین پاسخ را از همین یک‌بار بگیرید چندین بار الگوریتم را با مقداردهی‌های تصادفی اجرا کنید. به عبارت دیگر:

$$\begin{eqnarray} \text{For } &i& = 1 \text{ to } 100 \{ \\ &\quad& \text{Randomly initialize K-means}\\ &\quad& \text{Run K-means. Get } c^{(1)},...,c^{(m)}, \mu_1,...,\mu_K \\ &\quad& \text{Compute Cost Function (distortion)} \\ &\quad& J(c^{(1)},...,c^{(m)},\mu_1,...,\mu_k)\\ &\quad& \} \end{eqnarray}$$

معمولاً بین 50 تا 1000 بار الگوریتم K-means را اجرا می‌کنند. هر بار به‌صورت تصادفی مقداردهی اولیه‌ی الگوریتم K-means انجام می‌شود و پس از اجرای الگوریتم و به دست‌آوردن $c^{(1)},...,c^{(m)}$ و $\mu_1,...,\mu_k$ تابع هزینه را محاسبه می‌کنیم. در نهایت با مقایسه مقدار تابع هزینه برای تعداد دفعاتی که الگوریتم را اجرا کرده‌ایم کمترین مقدار $$J$$ را انتخاب می‌کنیم.

البته به یاد داشته باشید که این‌ کار در صورتی مفید است که تعداد خوشه‌های ما کم (بین 2 تا 10 خوشه) باشد. در صورتیکه تعداد خوشه‌ها زیاد (چند صد خوشه) باشد، به احتمال زیاد این‌ کار تفاوت چندانی را رقم نمی‌زند.

انتخاب تعداد خوشه‌ها

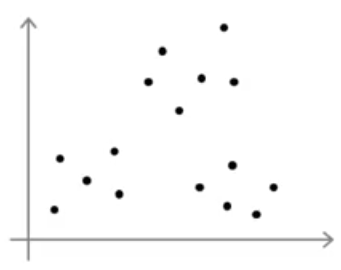
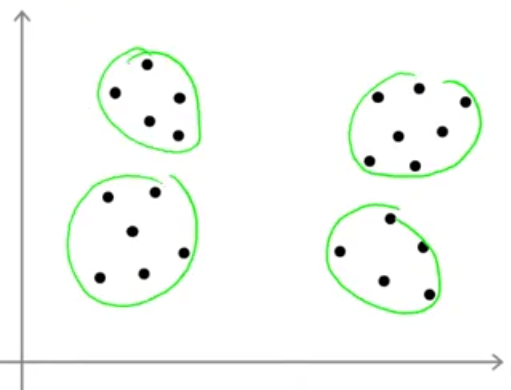
یکی از دلایل سخت بودن انتخاب تعداد خوشه‌ها آن است که معمولاً نمی‌توان به‌طور واضح خوشه‌های موجود در یک مجموعه داده را تشخیص داد. به عنوان مثال به داده‌های زیر نگاه کنید:

بعضی از شما ممکن است مانند شکل زیر 4 خوشه را تشخیص دهید:

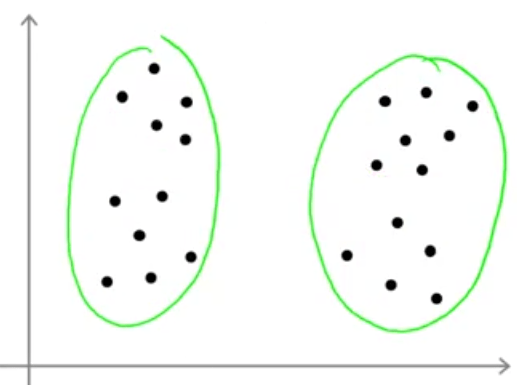
ولی بعضی دیگر مانند شکل زیر ممکن است 2 خوشه را تشخیص دهند:

یا تعداد دیگری داده‌ها را به 3 خوشه تقسیم کنند. بنابراین مشاهده می‌کنید که از روی داده‌ها نمی‌توان به‌صورت واضح تعداد خوشه‌ها را تشخیص داد یا به عبارت دیگر تنها یک جواب درست وجود ندارد. در حقیقت این یکی از مشکلات یادگیری بدون نظارت است؛ داده‌ها دارای برچسب نیستند که جواب درست مشخص باشد و این مسئله را برای ارائه‌ یک الگوریتم اتوماتیک که تعداد خوشه‌ها را مشخص کند بسیار سخت می‌کند. رایج‌ترین روش انتخاب تعداد خوشه‌ها به صورت دستی است ولی روش‌هایی هم برای انتخاب اتوماتیک تعداد خوشه‌ها وجود دارند که ممکن است در بعضی موارد مفید باشند.

روش بازو

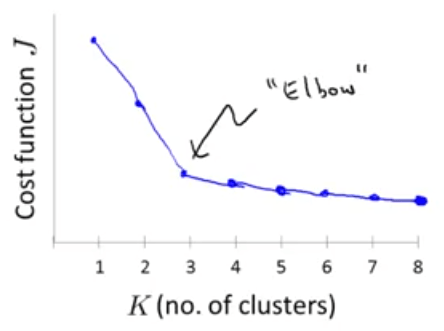
روش بازو یا "Elbow Method" یکی از روش‌هایی که ممکن است بتوان از روی آن تعداد خوشه‌ها را مشخص کرد. در این روش مقدار تابع هزینه را برحسب تعداد خوشه‌ها رسم می‌کنیم در این حالت ممکن است نموداری به شکل زیر داشته باشیم:

اگر به شکل دقت کنید یک بازوی واضح در نمودار را می‌توانید مشاهده کنید ( $$k=3$$ ). در حقیقت قبل از انتخاب 3 خوشه تابع هزینه روند نزولی نسبتا سریعی دارد ولی بعد از آن این روند بسیار کند شده است و می‌توان نتیجه گرفت که احتمالاً انتخاب 3 خوشه می‌تواند انتخاب مناسبی باشد.

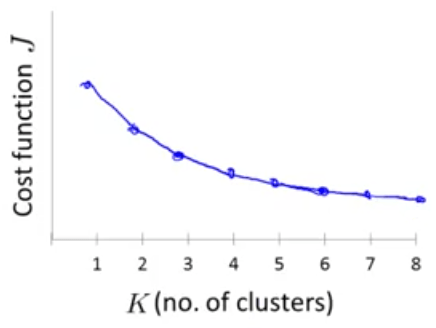
اگر همچنین نموداری داشته باشید، انتخابی معقول است که از روی روش بازو تعداد خوشه‌ها را انتخاب کنید. ولی بیشتر اوقات ممکن است نموداری شبیه نمودار زیر داشته باشید:

که در آن محل بازو دقیقا مشخص نیست. بنابراین به صورت خلاصه اگر بخواهیم روش بازو را ارزیابی کنیم باید گفت که ارزش امتحان کردن را دارد ولی لزوما نمی‌توان از این روش انتظار بالایی داشته باشیم.

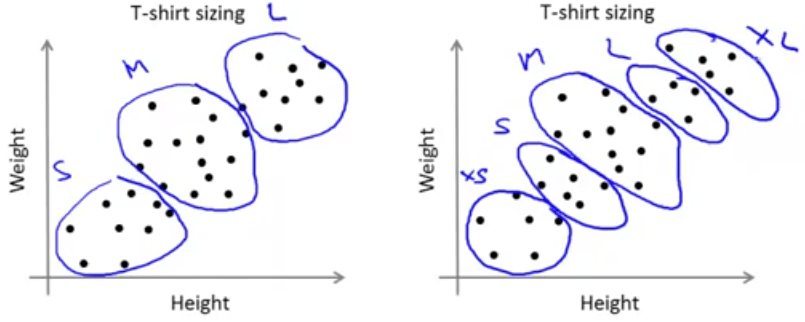
گاهی اوقات ممکن است که K-means را برای به‌دست آوردن خوشه‌هایی جهت استفاده برای اهدافی که در آینده دارید اجرا کنید. ارزیابی K-means براساس معیاری که نشان دهد که خوشه‌بندی به‌دست آمده چقدر خوب در جهت این اهداف عمل می‌کند، می‌تواند راهی برای انتخاب تعداد خوشه‌ها می‌باشد. برای نمونه به مثال تولیدی تی‌شرت برمی‌گردیم. ممکن است تصمیم بگیریم که $$k=3$$ یعنی سه اندازه کوچک (S)، متوسط (M) و بزرگ (L) داشته باشیم و یا تصمیم بگیریم که $$k=5$$ و پنج اندازه مختلف خیلی کوچک (XS)، کوچک (S)، متوسط (M)، بزرگ (L) و خیلی بزرگ (XL) را داشته باشیم.

برای انتخاب بین تعداد خوشه‌ها باید خودمان را جای تولید کننده‌ تی‌شرت بگذاریم و بررسی کنیم که کدامیک برای مشتریان تولیدی مناسب‌تر است و آن‌ها را خوشحال‌تر می‌کند و در نهایت براساس آنکه کدام یک برای تولیدی منطقی‌تر است، تعداد خوشه‌ها را انتخاب کنیم.

مثال دیگری از این نوع می‌تواند فشرده کردن یک عکس باشد که براساس تعداد خوشه‌ها بین کیفیت عکس و میزان فشرده شدن آن باید تصمیم بگیریم. یعنی ارزیابی K-means براساس هدف ما خواهد بود که آیا می‌خواهیم کیفیت عکس بهتر باشد یا حجم آن کمتر یا تعادلی بین این دو برقرار کنیم.

<< مبحث قبلی مبحث بعدی >>