Handling Skewed Data

<< مبحث قبلی مبحث بعدی >>

سنجش خطا برای مجموعه داده‌های نامتناسب

در بخش قبلی به این نتیجه رسیدیم که داشتن یک ارزیابی عددی جهت سنجش الگوریتم با آن بسیار ضروری است. در این بین موردی وجود دارد که ساختن یک ارزیابی عددی برای آن می‌تواند مشکل باشد و آن هم مورد کلاس‌های نامتناسب (skewed classes) است. به مثال زیر توجه کنید.

فرض کنید با استفاده از رگرسیون لجستیک می‌خواهیم نمونه‌های سرطان را دسته‌بندی کنیم (افرادی که دارای سرطان هستند \(y=1\) در برابر کسانی که سرطان ندارند \(y=0\)). بعد از اجرای الگوریتم متوجه می‌شویم که روی مجموعه داده‌های آزمایش تنها 1 درصد خطا داریم. به عبارت دیگر در 99 درصد موارد تشخیص ما درست بوده! در ظاهر الگوریتم فوق‌العاده‌ای داریم. ولی حالا بیاید فرض کنیم تنها %0.50 افراد موجود در مجموعه‌های آموزش و تست سرطان داشته باشند. در این حالت دیگر الگوریتم ما خیلی هم فوق‌العتده نیست و اگر کدی به مانند کد زیر که از نوع یادگیری هم نیست بنویسیم، حتی دارای خطای کمتر یعنی %0.50 خواهد بود که از الگوریتم یادگیری ما با خطای %1 هم بهتر است.

def predictCancer(x):
    y = 0 # ignore x!
    return y

به چنین حالت‌هایی که یکی از موارد مثبت یا منفی خیلی بیشتر از دیگری است skewed classes گفته می‌شود (یکی از کلاس‌ها بسیار بیشتر از دیگری است). در مثال بالا حالت مثبت در برابر حالت منفی بسیار نادر است. بنابراین اگر الگوریتم مانند کد بالا همواره \(y=0\) را پیش‌بینی کند، در ظاهر بسیار خوب عمل کرده است.

دیگر نمی‌توانیم تنها با یک عدد حقیقی الگوریتم خود را ارزیابی کنیم. یعنی در مثال بالا از دقت 99 درصد به دقت 99/5 درصد رسیدیم. ولی آیا دقت ما بیشتر شد یا فقط موارد \(y=0\) بیشتری را پیش‌بینی کردیم؟

پس ملاحظه می‌کنیم که در مورد skewed classes ارزیابی کردن الگوریتم کمی پیچیده‌تر است و باید یک معیار (Metric) دیگر برای آن تعریف کنیم.

Precision/Recall

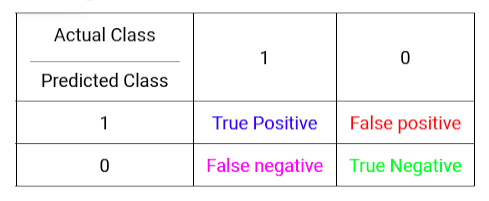
برای معرفی این معیار، ابتدا به جدول زیر دقت کنید. در ردیف افقی به مقادیر حقیقی کلاس دو عدد 1 و صفر به ترتیب برای بیمارانی که واقعا سرطان دارند و بیمارانی که در واقعیت سرطان ندارند اختصاص داده‌ایم. در طرف دیگر هم به آنچه که ما برای بیماران پیش‌بینی کرده‌ایم دو عدد 1 و صفر به ترتیب برای کسانی که پیش‌بینی کرده‌ایم سرطان دارند و برای بیمارانی که پیش‌بینی کرده‌ایم سرطان ندارند اختصاص داده‌ایم. حال در خانه‌های جدول با توجه به ترکیب واقعیت در برابر آنچه که ما پیش‌بینی کرده ایم 4 حالت ممکن را نوشته‌ایم.

  • مثبت درست: به درستی پیش‌بینی کرده‌ایم که دارای سرطان است.
  • مثبت اشتباه: به اشتباه پیش‌بینی کرده‌ایم که دارای سرطان است.
  • منفی اشتباه: به اشتباه پیش‌بینی کرده‌ایم که دارای سرطان نیست.
  • منفی درست: به درستی پیش‌بینی کرده‌ایم که دارای سرطان نیست.

حال با توجه به جدول فوق می‌توانیم Precision و Recall را به صورت زیر تعریف کنیم:

  • Precision: از بین همه بیمارانی که پیش‌بینی کرده ایم دارای سرطان هستند، چه کسری واقعا دارای سرطان هستند؟
    • $$ \text{Precision } = \frac{\text{True pos}}{\text{Predicted pos}} = \frac{\text{True pos}}{\text{True pos } + \text{ False pos} } $$
    $$ \text{Precision } = \frac{\text{True pos}}{\text{Predicted pos}} $$ $$ \quad \quad \quad \quad \quad \quad = \frac{\text{True pos}}{\text{True pos } + \text{ False pos} } $$
  • Recall: از بین همه بیمارانی که در واقعیت دارای سرطان هستند، چه کسری را به درستی دارای سرطان پیش‌بینی کرده‌ایم؟
    • $$ \text{Recall } = \frac{\text{True pos}}{\text{Actual pos}} = \frac{\text{True pos}}{\text{True pos } + \text{ False neg}} $$
    $$ \text{Precision } = \frac{\text{True pos}}{\text{Predicted pos}} $$ $$ \quad \quad \quad \quad \quad \quad = \frac{\text{True pos}}{\text{True pos } + \text{ False neg}} $$

بالا بودن مقدار هر دوی آنها نشان دهنده عملکرد خوب الگوریتم یادگیری است. همچنین در این حالت اگر همواره \(y=0\) را پیش‌بینی کنیم مقدار Recall برابر صفر خواهد بود و به ما می‌گوید که الگوریتم یادگیری مشکل دارد.

زمانی که از معیار Precision/Recall استفاده می‌کنید، به یاد داشته باشید که کلاس نادر (در اینجا افرادی که سرطان دارند) را \(y=1\) در نظر بگیرید.

مصالحه بین Precision و Recall

هنگام استفاده از معیار Precision/Recall لازم است که بین آنها مصالحه شود (trade off). در اینجا علاوه بر بحث در این مورد راه بسیار کارآمدتری جهت استفاده از این معیار برای سنجش الگوریتم‌های یادگیری را مطرح می‌کنیم.

اگر از رگرسیون لجستیک برای مثال تشخیص سرطان استفاده کنیم، معمولا به صورت زیر عمل خواهیم کرد:

  • predict 1 if \(h_{\theta}(x) \ge 0.50\)
  • predict 0 if \(h_{\theta}(x) \lt 0.50\)

فرض کنید می‌خواهیم تنها در حالتی \(y=1\) را پیش‌بینی کنیم که بسیار مطمئن باشیم (نمی‌خواهیم به بیمار شوک وارد شود و بعد از انجام درمان‌های بسیار سخت و گران قیمت مشخص شود که تشخیص اشتباه بوده). در این حالت به جای انتخاب آستانه (threshold) با مقدار 0.50 ممکن است مقدار 0.70 را انتخاب (یعنی با قاطعیت 70 درصد) یا مقدار 0.9 را انتخاب و با قاطعیت ۹۰ درصد به شخص بگوئیم که سرطان دارد. اگر چنین انتخاب‌هایی داشته باشیم با توجه به فرمول Precision خواهیم دید که مقدار آن بیشتر خواهد شد و در حقیقت با دقت بیشتری سرطان داشتن بیمار را پیش‌بینی می‌کنیم. اما از طرف دیگر با توجه به فرمول Recall هر چقدر که دقت ما بیشتر شود چون تعداد کمتری را به عنوان بیماران سرطانی معرفی می‌کنیم مقدار Recall کمتر خواهد شد.

حال عکس قضیه بالا را در نظر بگیرید. یعنی این بار نمی‌خواهیم که الکی به بیمار بگوئیم مشکلی ندارد در حالیکه ممکن است مشکل وجود داشته و نیاز به درمان داشته باشد (یعنی به فردی که ممکن است با تشخیص سریع سرطان درمان شود بگوئیم که مشکلی ندارد و دنبال درمان شدن نرود). در این حالت ممکن است مقدار آستانه را کمتر در نظر بگیریم مثلا برابر 0.30. با در نظر گرفتن چنین مقداری برای آستانه، مقدار Recall ما افزایش پیدا می‌کند در حالیکه این بار مقدار Precision ما کاهش می‌یابد.

بنابراین مشاهده می‌کنیم که انتخاب آستانه برای پیش‌بینی \(y=1\) تصمیم ساده‌ای نیست. بنابراین سوالی که در اینجا پیش می‌آید این است که آیا راهی برای انتخاب خودکار آستانه وجود دارد؟ یا به عبارت دیگر از بین مقادیر مختلف Precision/Recall که توسط الگوریتم‌های به کار برده شده به دست آمده است کدام یک را انتخاب کنیم؟

F1Score (F Score)

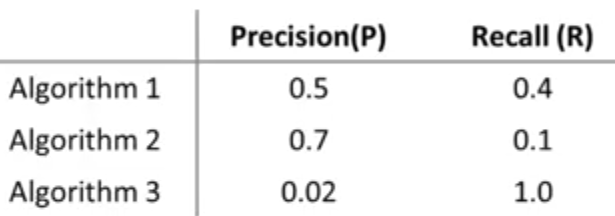
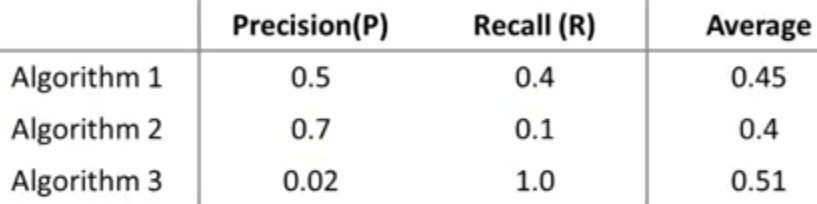
برای پاسخ به جواب سوال مطرح شده، لازم است دوباره به اهمیت داشتن یک عدد حقیقی که بتوانیم از روی آن قضاوت کنیم عملکرد الگوریتم ما چگونه است اشاره کنیم. مشکل ما در اینجا داشتن دو عدد به جای یک عدد حقیقی است. راهی که ممکن است به ذهن برسد، استفاده از مقدار میانگین Precision/Recall به جای هر یک از آنها است. ولی با نگاه به جدول زیر مشاهده می‌کنیم چنین انتخابی نمی‌تواند معقول باشد. زیرا طبق این انتخاب الگوریتم شماره 3 بهترین الگوریتم خواهد بود در حالیکه مقدار Precision برای آن بسیار کم است و مشابه حالتی است که الگوریتم ما تنها یکی از کلاس‌ها را پیش‌بینی کند (همواره \(y=1\)).

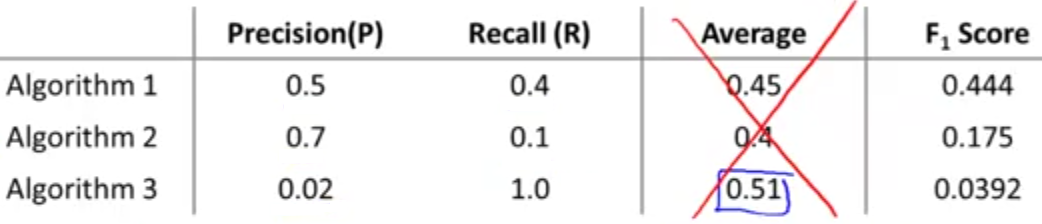
انتخاب معقول‌تر استفاده از فرمول زیر است که به مقدار F Score یا F1 Score شهرت دارد.

$$ F_1 Score = 2 \frac{PR}{P + R} $$

با دقت در فرمول بالا متوجه می‌شوید که اگر یکی از مقادیر Precision یا Recall صفر باشد، مقدار F Score هم صفر می‌شود و این نشانه بدترین عملکرد الگوریتم است. اما در حالت حدی دیگر اگر هر دو مقدار Precision و Recall برابر یک باشند، آنگاه مقدار F Score هم برابر یک می‌شود و این نشانه بهترین عملکرد الگوریتم یادگیری است.

بنابراین با استفاده از فرمول گفته شده می‌توانیم یک عدد حقیقی بین صفر و یک جهت ارزیابی الگوریتم خود داشته باشیم که بالاتر بودن آن به معنی عملکرد بهتر الگوریتم یادگیری است.

برای مثال بالا بر طبق مقادیر F Score الگوریتم اول بهترین عملکرد را دارد و مشاهده می‌کنیم که انتخاب آن از دید مقادیر Precision و Recall هم منطقی به نظر می‌رسد.

<< مبحث قبلی مبحث بعدی >>