Evaluating a Learning Algorithm

عیب یابی الگوریتم یادگیری

برای پیش بینی قیمت یک خانه از الگوریتم رگرسیون خطی منظم سازی شده به شکل زیر استفاده کردیم:

$$ J(\theta) = \frac{1}{2m} \left[\sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})^2 + \lambda \sum_{j=1}^{n} \theta_{j}^{2}\right] $$

حال فرض کنید بعد از به دست آوردن تابع فرضیه، آن را روی یک سری داده جدید تست می‌کنیم و متوجه خطای بزرگ و غیرقابل قبولی می‌شویم. سوال این است که قدم بعدی ما چیست؟

کارهایی که می‌توان انجام داد

جمع آوری داده بیشتر
آزمایش الگوریتم با تعداد خصوصیت کمتر
آزمایش الگوریتم با تعداد خصوصیت بیشتر
اضافه کردن جملات با درجه بالاتر $(x_{1}^{2}, x_{2}^{2}, x_{1}x_{2}, ...)$
آزمایش الگوریتم با کاهش لامبدا
آزمایش الگوریتم با افزایش لامبدا

اما نکته در این است که امتحان کردن هر یک از موارد بالا ممکن است تا ۶ ماه و بیشتر طول بکشد. بنابراین همین‌طوری نمی‌شود یکی از موارد بالا را انتخاب کرد.

بررسی الگوریتم یادگیری

در اینجا کلمه diagnostic را "بررسی" معنی کرده‌ایم ولی در واقع این کلمه در حوزه یادگیری ماشین چنین تعریف می‌شود: به اجرای تستی گفته می‌شود که به شما در به دست‌آوردن ایده‌ای درباره اینکه چه چیزی در مورد الگوریتم یادگیری کار می‌کند و یا نمی‌کند کمک نماید و راهنمایی باشد که چگونه عملکرد الگوریتم یادگیری را بهبود ببخشید.

هر چند اجرای بررسی الگوریتم یادگیری به زمان نیاز دارد ولی انجام آن می‌تواند استفاده خوبی از زمان باشد.

ارزیابی فرضیه

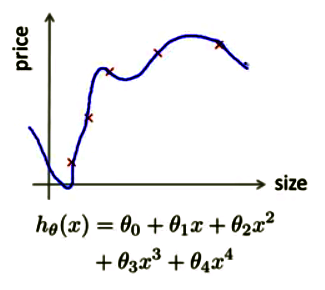
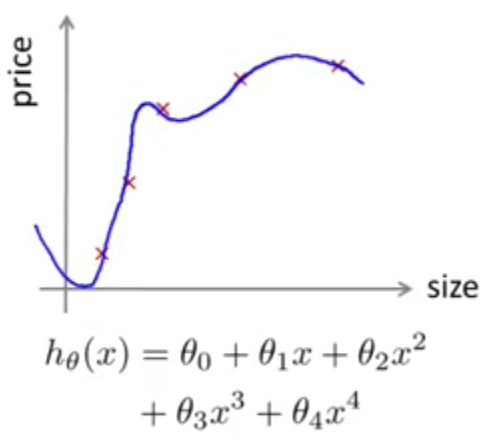
ممکن است فکر کنید که خطای کمتر در فرضیه محاسبه شده به معنی آن باشد که این فرضیه بهترین است. ولی اگر به یاد داشته باشید قبلاْ هم اشاره کردیم که چنین مطلبی صحت ندارد. به عنوان نمونه در شکل زیر نمودار به دست‌آمده به خوبی همه داده‌ها را برازش می‌‌کند وخطای آن صفر است اما همین نمودار را اگر بخواهیم به داده‌های جدید که در مجموعه داده‌های آموزش قرار ندارند، تعمیم دهیم با شکست مواجه خواهد شد. دلیل آن هم همان‌طور که می‌دانید به خاطر مسئله overfitting است.

اما از کجا متوجه شویم که با مشکل overfitting مواجه هستیم؟ بله! اگر مورد به مانند مثال مطرح شده ساده باشد می‌توان نمودار آن را رسم کرد ولی در حالت کلی که شاید بیش از 100 خصوصیت داشته باشیم، رسم نمودار غیر ممکن می‌شود و باید به دنبال راه دیگری بود.

راه استاندارد برای ارزیابی یک فرضیه

فرض کنید یک مجموعه داده به شکل زیر داریم:

size	price
2104	400
1600	330
2400	369
1416	232
3000	540
1985	300
1534	315
1427	199
1380	212
1494	243

کاری که باید انجام دهیم آن است که داده را به دو قسمت تقسیم کنیم؛ قسمت اول را به عنوان مجموعه داده آموزش و مجموعه دوم را به عنوان مجموعه داده تست نامگذاری و استفاده می‌کنیم. معمولاً برای قسمت اول 70 درصد از کل داده‌ها را انتخاب (داده‌های با زمینه طوسی در جدول بالا) و ۳۰ درصد بقیه (داده‌های با زمینه زرد در جدول بالا) را به عنوان مجموعه داده تست استفاده می‌کنیم. البته قبل از انتخاب بهتر است که داد‌ه‌ها را به صورت تصادفی مرتب کنیم.

فرایند آموزش / تست برای رگرسیون خطی

بعد از تقسیم داده‌ها به دو دسته آموزش و تست، نوبت به محاسبه فرضیه و ارزیابی آن می‌رسد. در اینجا مطلب را برای رگرسیون خطی توضیح می‌دهیم، ولی روند کار برای سایر الگوریتم‌ها نیز به همین نحو می‌باشد.

با استفاده از 70 درصد از کل داده‌ها (مجموعه داده‌های آموزش) پارامتر $\theta$ را محاسبه می‌کنیم (کمینه کردن خطای آموزش $J(\theta)$ )

۲-محاسبه خطای مجموعه داده‌های تست:

$$ J_{test}(\theta) = \frac{1}{2m_{test}} \sum_{i=1}^{m_{test}} (h_{\theta}(x^{(i)}_{test}) - y^{(i)}_{test})^2 $$

برای logistic regression هم به صورت مشابه عمل می‌کنیم، فقط می‌بایست $J(\theta)$ مربوط به آن را محاسبه کنیم. ولی بعضی اوقات یک راه جایگزین وجود دارد که می‌تواند برای تفسیر ساده‌تر باشد. این راه جایگزین محاسبه خطای طبقه‌بندی اشتباه است؛ به این معنی که بررسی کنید مثال را درست حدس زده‌اید یا خیر. این خطا به شکل زیر محاسبه می‌شود:

$$ err(h_{\theta}(x), y) = \begin{cases} 1 \quad \quad \text{if} \quad \quad h_{\theta}(x) \ge 0.5, \quad y = 0 \\ {} \quad \quad \quad \quad \quad \quad \quad \quad \text{or} \\ {} \quad \quad \quad \quad \quad h_{\theta}(x) \le 0.5, \quad y = 1 \\ 0 \quad \quad \text{otherwise} \end{cases} $$ $$ \text{Test error} = \frac{1}{m_{test}} \sum_{i=1}^{m_{test}} err(h_{\theta}(x^{(i)}), y^{(i)}) $$

بنابراین با استفاده از این روش و محاسبه مقدار $J_{test}(\theta)$ برای فرضیه به دست آمده از الگوریتم می‌توان ایده‌ای از میزان خوبی یا بدی آن داشته باشیم. در بخش بعدی به این مطلب بیشتر خواهیم پرداخت.

انتخاب مدل

فرض کنید می‌خواهید تصمیم بگیرد که چند جمله‌ای با چه درجه‌ای استفاده کنید و یا می‌خواهید در مورد انتخاب پارامتر منظم‌سازی تصمیم‌گیری کنید، چگونه این کار را انجام می‌دهید؟ این مسائل را مشکلات انتخاب مدل می‌گویند. در اینجا با بحث در مورد چگونگی تقسیم مجموعه داده‌ها به سه بخش آموزش، اعتبارسنجی و آزمایش (تست) راه‌هایی را برای چگونگی انتخاب مدل یاد خواهیم گرفت.

در فصل‌های قبل بارها مشکل overfitting را مطرح کردیم و دیدیم که خوب بودن برازش داده‌ها توسط الگوریتم یادگیری به معنی خوب بودن فرضیه ما نیست. به همین جهت اندازه خطایی که از مجموعه آموزش اندازه‌گیری می‌شود، مقیاس خوبی برای سنجش فرضیه به دست آمده نیست.

به عبارت بهتر بعد از اینکه پارامترهای $\theta_0,\theta_1,...,\theta_4$ را به تعدادی داده برازش دهیم (مثلا مجموعه داده آموزش)، خطای پارامترها که روی همان مجموعه داده اندازه‌گیری می‌شود (خطای یادگیری $J(\theta)$ ) به احتمال زیاد کمتر از خطای واقعی تعمیم آن (استفاده از آن روی داده‌های جدید) است.

فرض کنید در مسئله انتخاب مدل، مشکل شما انتخاب درجه چند جمله‌ای است که می‌خواهید به کار ببرید. آیا از یک چند جمله‌ای خطی، درجه دو و یا با درجات بالاتر تا درجه 10 می‌خواهید استفاده کنید؟

$$ 1. h_{\theta}(x) = \theta_0 + \theta_1x $$ $$ 2. h_{\theta}(x) = \theta_0 + \theta_1x + \theta_2x^2 $$ $$ 3. h_{\theta}(x) = \theta_0 + \theta_1x + \theta_2x^2 + \theta_3x^3 $$ $$ \vdots $$ $$ 10. h_{\theta}(x) = \theta_0 + \theta_1x + ... + \theta_{10}x^{10} $$

پس در اینجا علاوه بر پارامترهای $\theta$ پارامتر جدیدی که درجه چند جمله‌ای را برای ما مشخص می‌کند و آن را با $$d$$ نشان می‌دهیم، باید در نظر گرفته شود. پس در این مثال مقدار $$d$$ از یک تا 10 تغییر می‌کند.

یکی از راه‌های انتخاب مقدار $$d$$ آن است که برای هر مدل تابع هزینه را کمینه کنیم و یک مجموعه از پارامترها را محاسبه نمائیم $(\theta^{(1)},...,\theta^{(10)})$ . سپس هر یک از این فرضیه‌ها به دست‌ آمده را روی مجموعه داده آزمایش (تست) امتحان کنیم و مقادیر $J_{\text{test}}(\theta^{(1)}),...,J_{\text{test}}(\theta^{(10)})$ را به دست آوریم. از بین مقادیر به دست آمده هر کدام که کمترین مقدار را داشته باشد، انتخاب می‌کنیم. در این مثال فرض کنید مقدار $J_{\text{test}}(\theta^{(5)})$ کمترین مقدار را دارد و چند جمله‌ای درجه 5 را به عنوان مدل خود انتخاب می‌کنیم. سوال این است که این مدل تا چه اندازه به خوبی می‌تواند تعمیم پیدا کند؟

پاسخ آن است که به احتمال زیاد $J_{\text{test}}(\theta^{(5)})$ نمی‌تواند تخمین خوبی از عمومیت دادن به فرضیه باشد و دلیل آن هم واضح است. زیرا در اینجا دقیقا با همان مشکل انتخاب $\theta$ در مرحله اول مواجه هستیم. در مرحله اول با کمینه کردن تابع هزینه مقادیر پارامتر $\theta$ را به دست آوردیم ولی از آنجایی که خطا برای همان مجموعه داده‌ای که از آنها $\theta$ را محاسبه کردیم اندازه‌گیری می‌شود پس $J(\theta)$ نمی‌تواند قابل اعتماد باشد. در اینجا هم $$d$$ را بر اساس بهترین جواب ممکن برای مجموعه آزمایش (تست) به دست آورده‌ایم، بنابراین انتخاب $\theta^{(5)}$ جهت تعمیم دادن فرضیه بسیار خوشبینانه است.

برای حل این مشکل داده‌های اولیه را به جای دو دسته به سه دسته تقسیم می‌کنیم. دسته آموزش، دسته اعتبارسنجی و دسته آزمایش (تست). برای این کار %60 داده‌ها را به مجموعه آموزش (داده‌های با زمینه خاکستری در جدول زیر)، %20 را به دسته اعتبارسنجی (داده‌های با زمینه زرد در جدول زیر) و %20 پایانی را به مجموعه آزمایش (تست) (داده‌های با زمینه سبز در جدول زیر) اختصاص می‌دهیم. البته این تقسبم بندی رایج است ولی سهم هر مجموعه می‌تواند متفاوت از اعداد گفته شده باشد.

size	price
2104	400
1600	330
2400	369
1416	232
3000	540
1985	300
1534	315
1427	199
1380	212
1494	243

دسته اعتبارسنجی validation یا گاهی cross validation گفته می‌شود و معمولا آن را به صورت مخفف cv نشان می‌دهند.

حال می‌توان خطای هر یک را محاسبه کرد:

$$ J_{training}(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h_{\theta}(x^{(i)}) - y^{(i)})^2 $$ $$ J_{cv}(\theta) = \frac{1}{2m_{cv}} \sum_{i=1}^{m_{cv}} (h_{\theta}(x^{(i)}_{cv}) - y^{(i)}_{cv})^2 $$ $$ J_{test}(\theta) = \frac{1}{2m_{test}} \sum_{i=1}^{m_{test}} (h_{\theta}(x^{(i)}_{test}) - y^{(i)}_{test})^2 $$

با این تقسیم بندی برای محاسبه $$d$$ باید به شکل زیر عمل کرد:

$$ 1. \min_{\theta} J(\theta) \rightarrow \theta^{(1)} \xrightarrow {\text{test on cv}} J_{cv}(\theta^{(1)}) $$ $$ 2. \min_{\theta} J(\theta) \rightarrow \theta^{(2)} \xrightarrow {\text{test on cv}} J_{cv}(\theta^{(2)}) $$ $$ \vdots $$ $$ 10. \min_{\theta} J(\theta) \rightarrow \theta^{(10)} \xrightarrow {\text{test on cv}} J_{cv}(\theta^{(10)}) $$

از بین مقادیر به دست آمده کمترین مقدار را انتخاب می‌کنیم، مثلا $J_{cv}(\theta^{(4)})$ . به عبارت دیگر مدل را به ازای $$d = 4$$ انتخاب می‌کنیم. بعد از انتخاب مدل، آن را روی مجموعه داده آزمایش (تست)، امتحان می‌کنیم. از آنجا که $$d$$ را از روی $J_{cv}$ به دست آورده‌ایم، می‌توان گفت که دیگر $$d$$ را به مجموعه آزمایش (تست) برازش نداده‌ایم و می‌توانیم عمومیت دادن به رابطه به دست آمده را امتحان کنیم.

<< مبحث قبلی مبحث بعدی >>