Dimensionality Reduction
فشردهسازی سازی داده
نوع دیگری از یادگیری بدون نظارت کاهش بعد (Dimensionality Reduction) است. دلایل متعددی برای استفاده از کاهش بعد وجود دارد. یکی از این دلایل فشردهسازی داده است. فشردهسازی داده چنانکه در بخشهای بعدی خواهیم دید نه تنها باعث کاهش استفاده از حافظه خواهد شد بلکه سرعت اجرای الگوریتم را هم بالا میبرد.
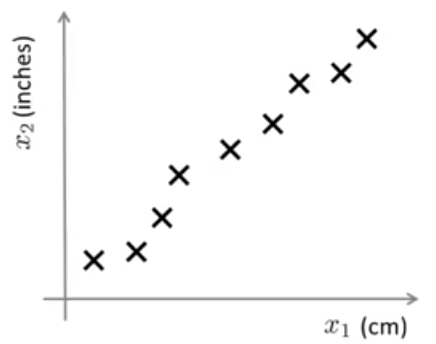
فرض کنید مسئلهای به ما داده شده که دارای خصوصیات بسیار زیادی است. دو تا از این خصوصیات در مورد طول را در شکل زیر رسم کردهایم. هر دوی این خصوصیتها طول را نمایش میدهند، یکی برحسب سانتیمتر و دیگری برحسب اینچ. داشتن هر دوی این خصوصیتها داده تکراری است زیرا هر دو طول را اندازهگیری میکنند. بنابراین بهجای داشتن این دو خصوصیت شاید بتوان یک خصوصیت را معرفی کرد، به عبارت دیگر بهجای داشتن یک داده دو بعدی یک داده یک بعدی داشته باشیم.
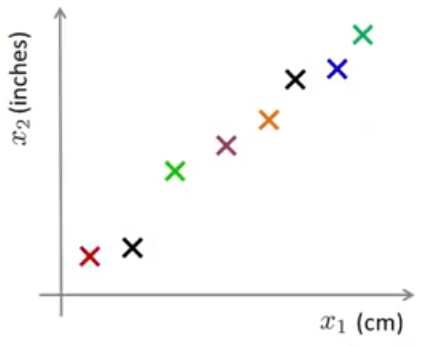
هرگاه دادههایی داشته باشیم که ارتباط تنگاتنگی باهم داشته باشند، احتمالاً بخواهیم که از کاهش بعد استفاده کنیم و از تکرار بیخودی دادهها جلوگیری نمائیم. اما بیایید نگاهی عمیقتر به مسئله کاهش بعد بیاندازیم. شکل قبلی را در زیر مشاهده میکنید با این تفاوت که در اینجا دادهها را بهصورت رنگی نمایش دادهایم.
،با کاهش بعد منظورمان این است که میخواهیم مثلاً خطی به مانند خط سبز رنگ در شکل زیر پیدا همه دادهها را روی آن تصور و مکان هر یک از دادهها را روی آن اندازهگیری کنیم.
\(z_1\) خصوصیت جدید ما است. به این شکل که اگر قبلا مثلا \(x^{(1)} \in mathbb{R}^2\) یعنی نیاز به دو عدد برای معرفی داشت الان \(z^{(1)} \in mathbb{R}\) و تنها نیاز به یک عدد حقیقی دارد. برای بقیه دادهها هم به همین شکل. بنابراین الان برای هر داده به جای دو عدد تنها نیاز به ذخیره یک عدد داریم و به عبارتی حافظه مورد استفاده را به نصف کاهش دادهایم.
میتوان کاهش بعد را از 3 بعد به 2 بعد هم انجام داد و یا ممکن است که دادههای ما \(1000D\) باشند و با کاهش بعد آنها را به \(100D\) کاهش دهیم. ولی برای نمایش همچنین حالتی محدودیت داریم و نمیتوانیم چنین حالتی را نمایش دهیم.
نمایش دادهها
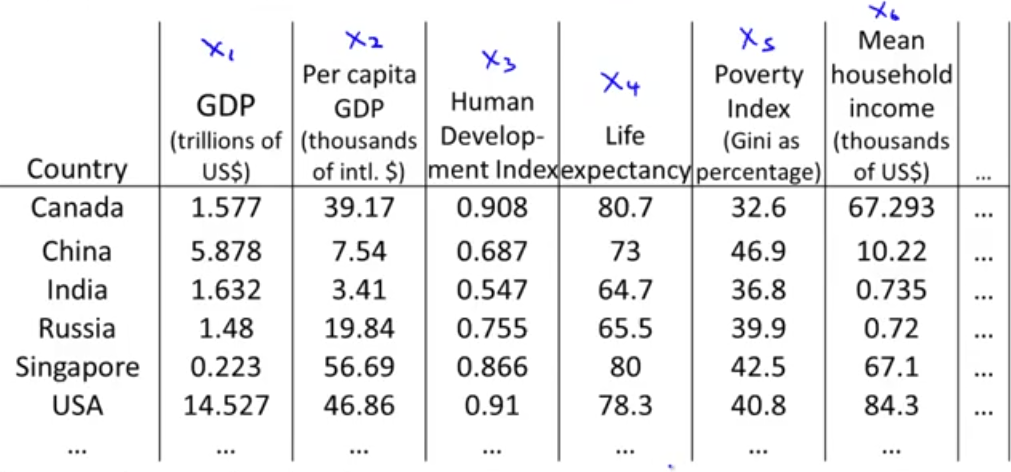
در بخش قبل از کاهش بعد برای فشردهسازی داده استفاده کردیم. در این بخش کاربرد دیگر آن یعنی به تصویر کشیدن (visualization) را میخواهیم بررسی کنیم. در مسائل یادگیری ماشین اگر بتوانیم دادههایمان را بهتر درک کنیم و راهی برای نمایش آنها داشته باشیم به ما در بهکار بردن الگوریتمهای یادگیری موثر کمک میکند. فرض کنید دادههایی به شکل زیر داریم:
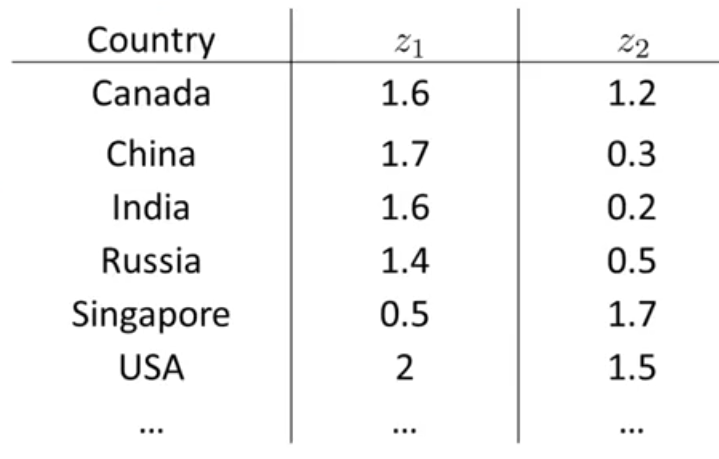
در این جدول برای هر کشور تنها توانستهایم در حدود 6 خصوصبت را نمایش دهیم. ولی در واقع این جدول شامل 50 خصوصیت است. به عبارت دیگر برای توصیف هر کشور 50 عدد استفاده شده و \(x \in \mathbb{R}^{50}\). است. حال فرض کنید توانستهایم بهجای این 50 عدد برای هر کشور تنها از 2 خصوصیت استفاده کنیم به شکل زیر:
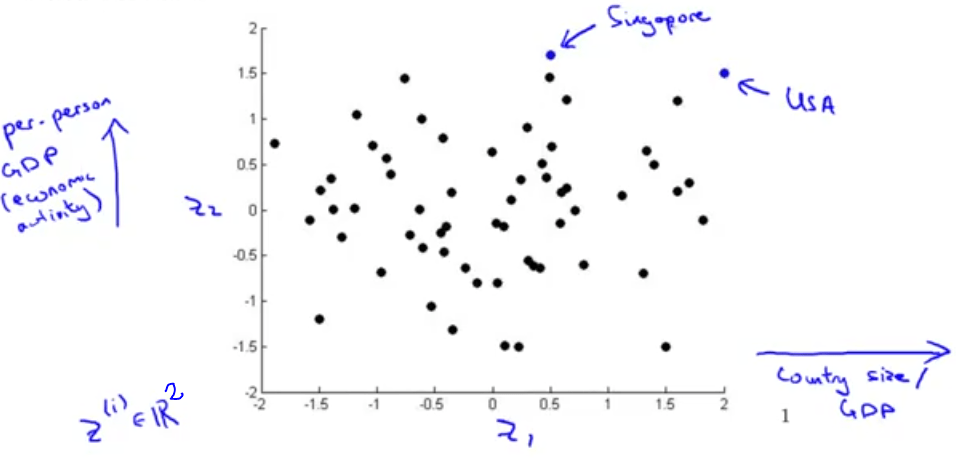
اگر بتوانیم چنین کاری را انجام دهیم، میتوان دادهها را رسم کرد و ایده بهتری داشته باشیم.البته خروجی خصوصیتهای جدید ممکن است بهصورت خاص بیانگر معنی خاصی نباشند و معمولاً به ما مربوط میشود که تشخیص دهیم این ویژگیهایی حدودا میتوانند بیانگر چه چیزی باشند. مثلا اگر دادههای جدید را رسم کنیم:
میتوان حدس زد که محور افقی میتواند مرتبط به اندازه کشور یا اندازه فعالیتهای اقتصادی یک کشور باشد و محور عمودی مربوط به فعالیتهای اقتصادی برای هر فرد باشد. مثلا نقطهی مشخص شده برای آمریکا نشان میدهد که هم فعالیت اقتصادی کل و هم فعالیت اقتصادی به ازای هر نفر بالایی دارد ولی برای سنگاپور هرچند فعالیت اقتصادی برای هر نفر بالا است اما فعالیت اقتصادی کل آن پایین است. زیرا از آمریکا خیلی کوچکتر است. در حقیقت در بین 50 خصوصیت داده شده این دو خصوصیت منبع اصل تغییرات هستند.
بنابراین مشاهده میکنیم که با کاهش خصوصیت از \(50D\) به \(2D\) میتوانیم دادهها را نمایش دهیم و درک بهتری از آن داشته باشیم.
برای مسئله کاهش بعد با اختلاف زیاد الگوریتم PCA که مخفف کلمات Principal Component Analysis است، بیشترین استفاده را دارد. که در بخش بعدی در مورد آن بحث خواهیم کرد.