Density Estimation

توزیع گاوسین

فرض کنید $x \in \mathbb{R}$ . اگر توزیع $$x$$ گاوسین با میانگین $\mu$ و واریانس $\sigma^2$ باشد، به بیان ریاضی آن را به شکل زیر نمایش می‌دهند:

$$x \sim \mathcal{N}(\mu, \sigma^2)$$

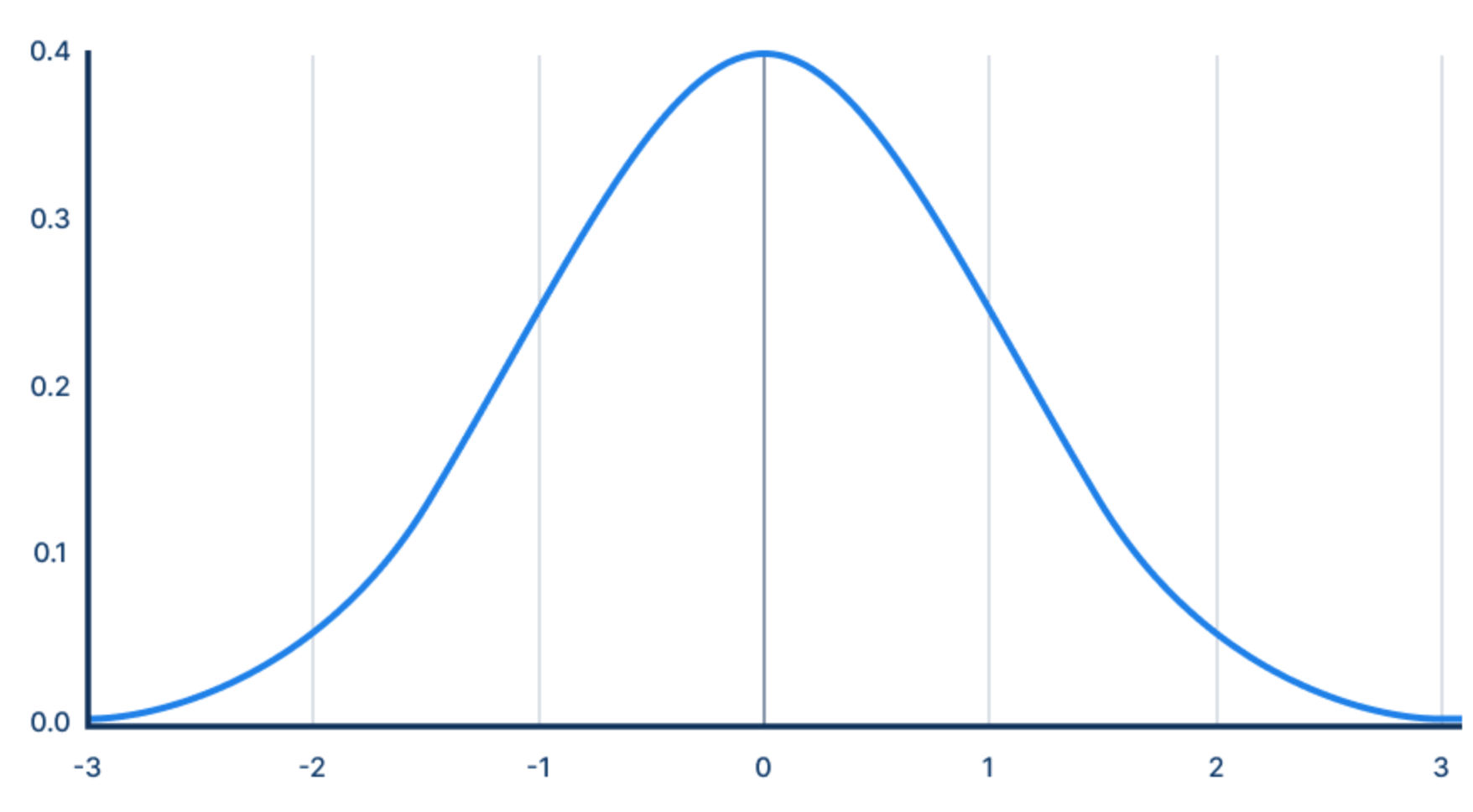
که نمودار آن به صورت زیر خواهد بود و بیانگر احتمال مقادیری است که $$x$$ می‌تواند داشته باشد.

فرمول توزیع گاوسین (نمودار بالا) به شکل زیر است:

$$p(x;\mu,\sigma^2) = \frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(x-\mu)^2}{2\sigma^2})$$

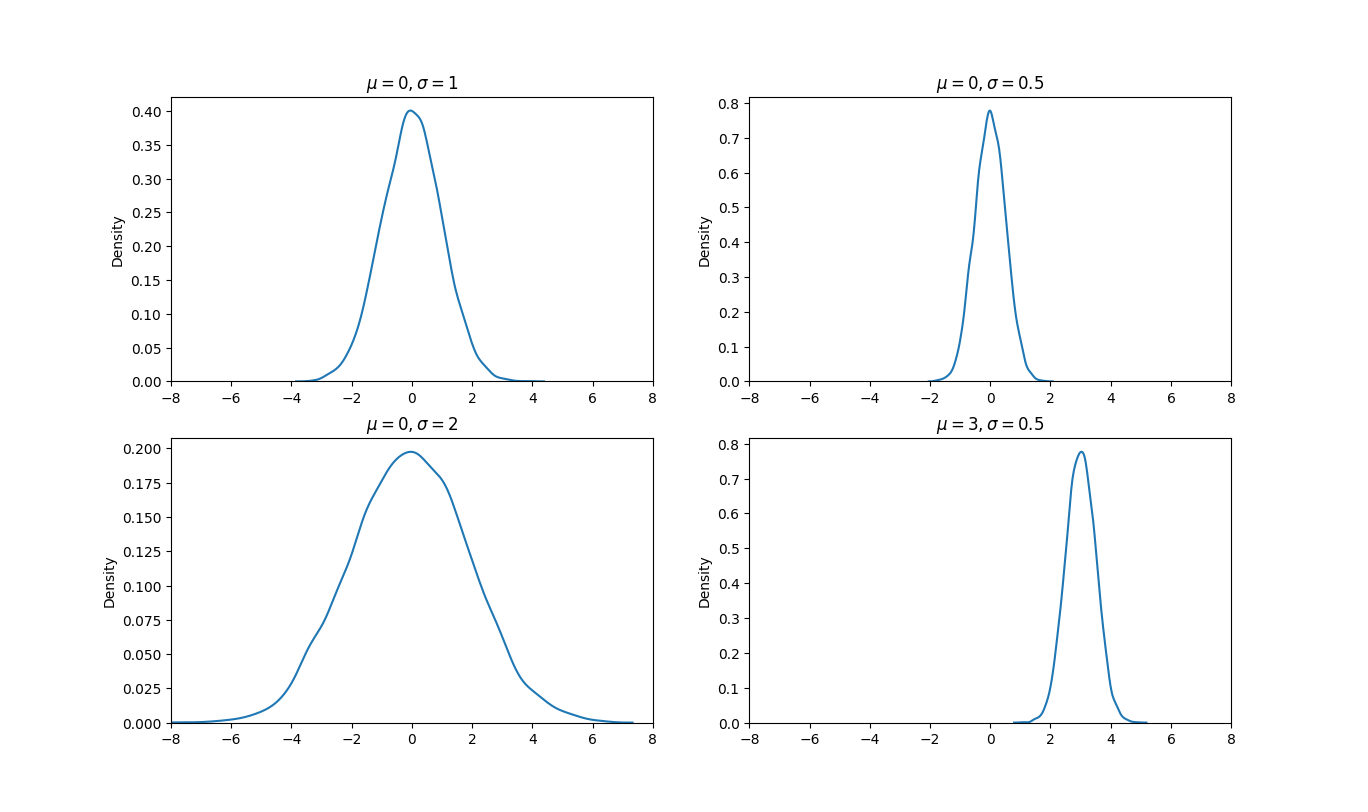
مثال‌هایی از توزیع گاوسین

با دقت در نمودارهای بالا متوجه خواهیم شد که مقدار $\mu$ (میانگین) مرکز تقارن منحنی را مشخص می‌کند. همچنین مشاهده می‌کنید هر چقدر $\sigma$ (انحراف معیار) کوچک‌تر باشد، نمودار توزیع گاوسین باریک‌تر، بلندتر و دارای شیب تندتری است و هر چقدر $\sigma$ بیشتر باشد نمودار پهن‌تر و کوتاه‌تر خواهد بود.

مسئله تخمین پارامترها

فرض کنید که مجموعه داده‌ای به شکل زیر داریم:

$$\{x^{(1)}, x^{(2)}, ..., x^{(m)}\} \quad x^{(i)} \in \mathbb(R)$$

و فرض کنید که هر یک از داده‌های $x^{(i)}$ ما بر اساس یک توزیع گاوسین با $\mu$ و $\sigma$ مشخص باشند:

$$x^{(i)} \sim \mathcal{N}(\mu,\sigma^2)$$

مانند داده‌های شکل زیر:

مسئله ما این است که چه نمودار توزیع نرمالی بهترین توصیف را از این مجموعه داده خواهد داشت؟ به عبارت دیگر مسئله ما یافتن پارامترهای $\mu$ و $\sigma$ است که برای تعیین آنها به شکل زیر عمل می‌کنیم:

$$\mu = \frac{1}{m} \sum^{m}_{i=1} x^{(i)}$$

$$\sigma^2 = \frac{1}{m} \sum^{m}_{i=1} (x^{(i)} - \mu)^2$$

مسئله تخمین چگالی

مسئله تخمین چگالی، همان یافتن مدل $$p(x)$$ است. فرض کنید یک مجموعه داده به صورت زیر داشته باشیم:

$$\{x^{(1)}, x^{(2)}, ..., x^{(m)}\} \quad x^{(i)} \in \mathbb(R)^n$$

و هر یک از خصوصیات مسئله از یک توزیع گاوسین پیروی کنند یعنی:

$$x_1 \sim \mathcal{N}(\mu_1,\sigma^{2}_{1})$$

$$x_2 \sim \mathcal{N}(\mu_2,\sigma^{2}_{2})$$

...

$$x_n \sim \mathcal{N}(\mu_n,\sigma^{2}_{n}),$$

در این حالت مدل $$p(x)$$ برای این مجموعه داده را به شکل زیر تعریف می‌کنیم:

$$ p(x) = p(x_1;\mu_1,\sigma^{2}_{2}) p(x_2;\mu_2,\sigma^{2}_{2})... p(x_n;\mu_n,\sigma^{2}_{n}) $$

اگر با آمار و احتمالات آشنا باشید، می‌دانید که تابع احتمال معرفی شده در بالا با فرض مستقل بودن $$x$$ ها است ولی الگوریتمی که می‌خواهیم معرفی کنیم در هر صورت چه $$x$$ ها از هم مستقل باشند و یا نباشند بوسیله تعریف بالا به خوبی کار می‌کند. رابطه معرفی شده برای $$p(x)$$ را می‌توان به صورت فشرده زیر با استفاده از علامت $\prod$ برای حاصلضرب به صورت زیر نوشت:

$$p(x) = \prod_{j=1}^{n} p(x_j;\mu_j,\sigma^{2}_{j})$$

الگوریتم یافتن بی هنجاری

خصوصیت $$x_j$$ راکه به نظر شما ممکن است نمایش دهنده نمونه‌های بی هنجار باشد انتخاب کنید.
پارامترهای $\mu_1, \mu_2,...,\mu_n$ و $\sigma_1, \sigma_2,...,\sigma_n$ را محاسبه کنید.
$$\mu_j = \frac{1}{m} \sum^{m}_{i=1} x^{(i)}_{j}$$

$$\sigma^{2}_{j} = \frac{1}{m} \sum^{m}_{i=1} (x^{(i)}_{j} - \mu_{j})^2$$
وقتی یک مثال جدید $$x$$ را دارید، $$p(x)$$ را محاسبه کنید.
$$\begin{eqnarray} p(x) &=& \prod_{j=1}^{n} p(x_j;\mu_j,\sigma^{2}_{j}) \\ &=& \prod_{j=1}^{n} \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(x_j - \mu_j)^2}{2\sigma^{2}_{j}}) \end{eqnarray}$$
اگر $p(x) \lt \epsilon$ باشد نمونه بی هنجاراست.

<< مبحث قبلی مبحث بعدی >>