Collaborative Filtering

فیلتر مشارکتی

در این بخش رویکرد دیگری برای ساختن یک سیستم پیشنهاد کننده به اسم Collaborative Filtering را معرفی می‌کنیم. این الگوریتم یک ویژگی بسیار جالب دارد و آن یادگیری خصوصیت‌ها است؛ یعنی الگوریتم خودش یاد می‌گیرد که کدام خصوصیت‌ها را استفاده کند.

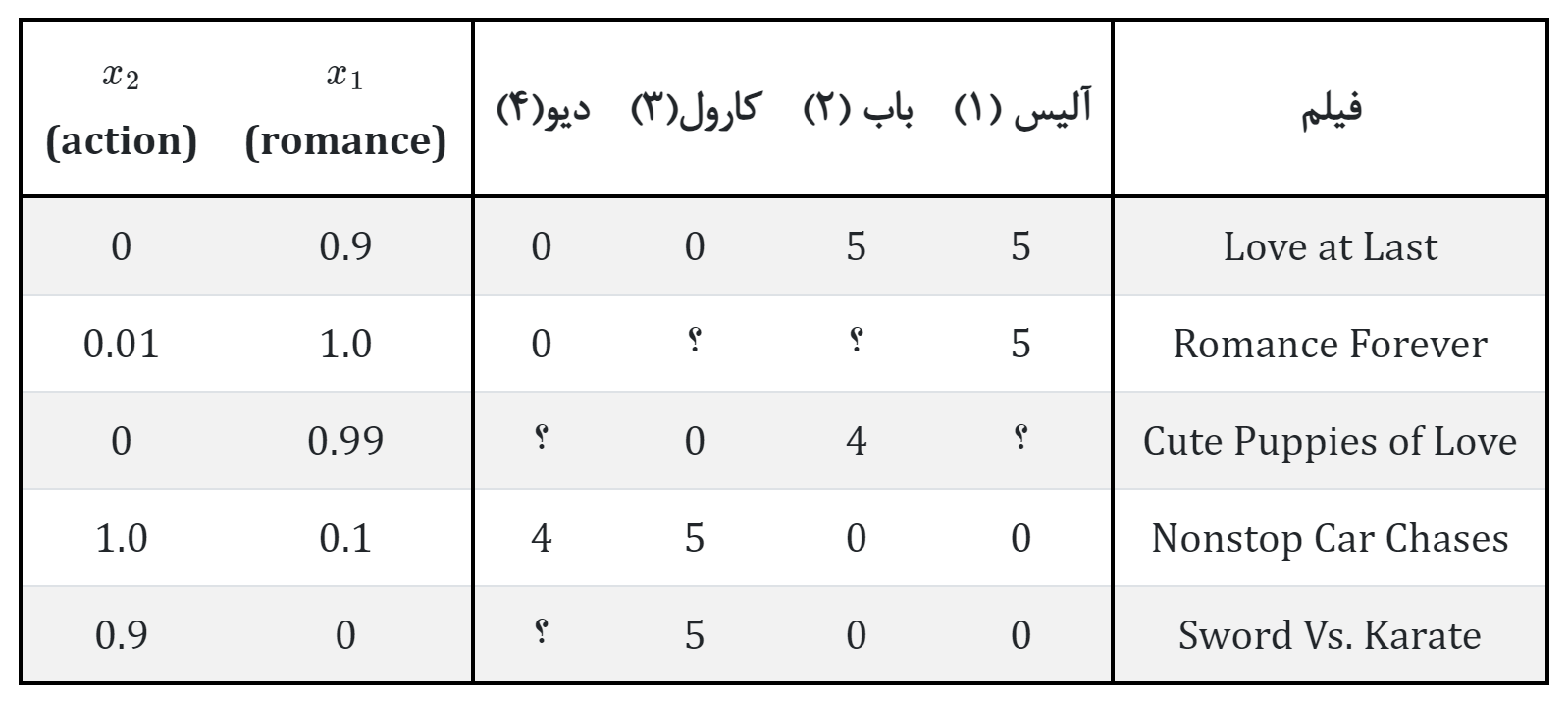
در مثال بخش قبلی این مجموعه داده را داشتیم:

واضح است که به دست آوردن اطلاعات خصوصیات $$x_1$$ و $$x_2$$ می‌تواند برای ما بسیار گران تمام شود. به این معنی که کسی وجود داشته باشد همه فیلم‌ها را نگاه کند و به لحاظ رمانتیک یا اکشن بودن عددی به آن فیلم‌ها اختصاص دهد. ضمن آنکه معمولا خیلی بیش از این دو خصوصیت را لازم خواهیم داشت.

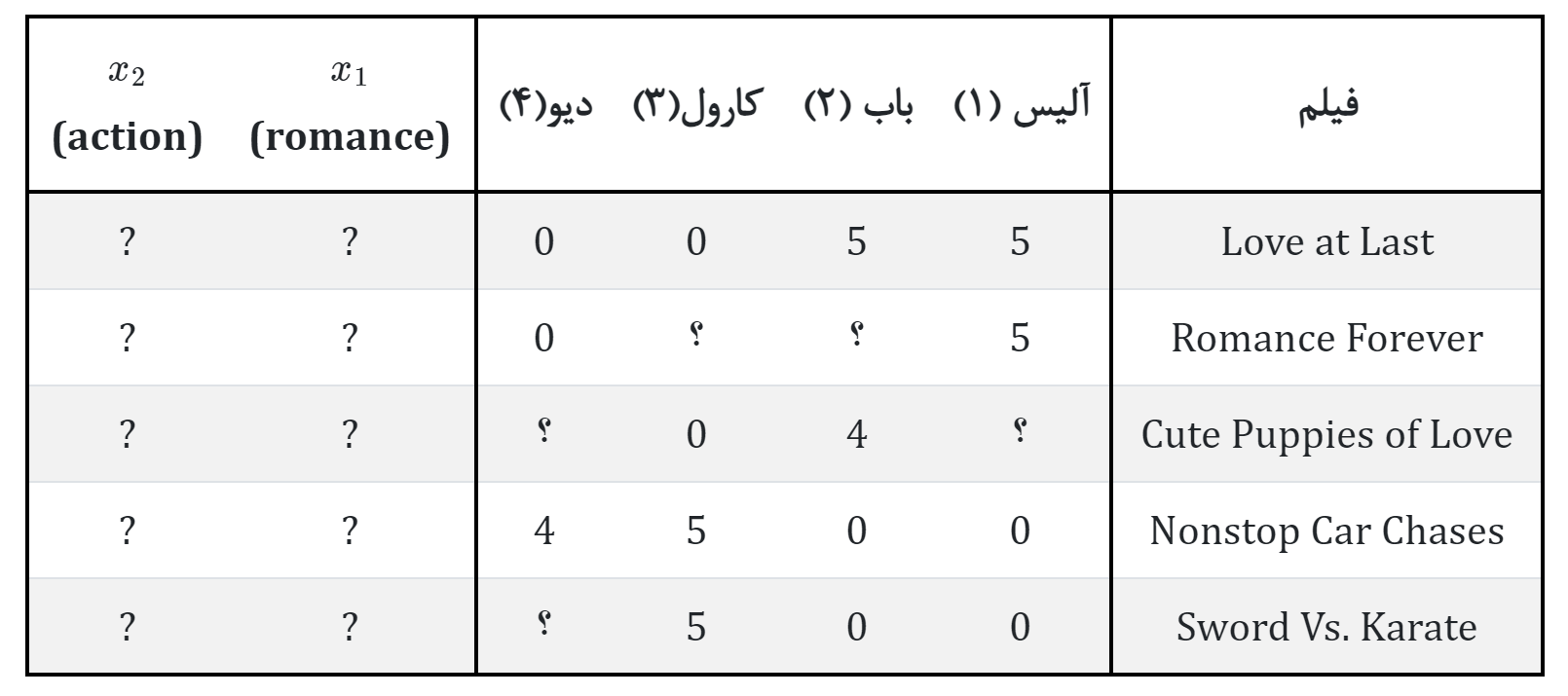
پس بیائید کمی مسئله را عوض کنیم و فرض کنیم مقادیر $$x_1$$ و $$x_2$$ را نداریم.

اما هر یک از کاربران مشخص می‌کنند که تا چه اندازه مثلا فیلم رمانتیک یا اکشن را دوست دارند. به طور مثال اگر پارامترهای $\theta^{(1)},\theta^{(2)},\theta^{(3)},\theta^{(4)},$ به ترتیب پارامترهای مربوط به آلیس، باب، کارول و دیو باشند:

$$ \theta^{(1)} = \begin{bmatrix} 0 \\ 5 \\ 0 \end{bmatrix} \quad \theta^{(2)} = \begin{bmatrix} 0 \\ 5 \\ 0 \end{bmatrix} $$ $$ \theta^{(3)} = \begin{bmatrix} 0 \\ 0 \\ 5 \end{bmatrix} \quad \theta^{(4)} = \begin{bmatrix} 0 \\ 0 \\ 5 \end{bmatrix} $$

که عدد 5 میزان حداکثر علاقه را نشان می‌دهد. اگر بتوانیم از کاربران خود چنین اطلاعاتی بگیریم، آنگاه می‌توان مقادیر $$x_1$$ و $$x_2$$ از طریق این اطلاعات به دست آوریم

مثلا اگر به فیلم اول در جدول نگاه کنید، این فیلم از آلیس و باب که فیلم‌های رمانتیک را دوست دارند، نمره بالایی گرفته ولی کارول و دیو که به فیلم‌های اکشن علاقه دارند و از فیلم‌های رمانتیک بدشان می‌اید نمره پائینی گرفته است. پس می‌توان نتیجه گرفت که این فیلم، یک فیلم رمانتیک است و اکشنی در آن وجود ندارد.

حال بیائید این مسئله را فرمول‌بندی کنیم. با داشتن $\theta^{(1)},\theta^{(2)},...,\theta^{(n)},$ ، برای یادگیری $x^{(i)}$ باید:

$$\begin{eqnarray} \min_{x{(i)}} \frac{1}{2} &\sum&_{j:r(i,j)=1} \left((\theta^{(j)})^Tx^{(i)}-y^{(i,j)}\right)^2\\ &+&\frac{\lambda}{2}\sum_{k=1}^{n}(x^{(i)}_{k})^2 \end{eqnarray}$$

هدف ما کمینه کردن جمله اول است. یعنی خصوصیت‌هایی را انتخاب کنیم که مقدار پیش‌بینی شده برای خصوصیت $$i$$ توسط کاربر $$j$$ به لحاظ خطایی خیلی از مقدار واقعی‌ای که کاربر $$j$$ به فیلم $$i$$ داده است دور نباشد. جمله دوم هم که همان جمله منظم سازی است.

عبارت بالا یک خصوصیت را برای یک فیلم یاد می‌گیرد ولی چیزی که ما نیاز داریم یادگیری همه خصوصیت‌های $x^{(1)},...,x^{(n_m)}$ برای همه فیلم‌ها است. بنابراین عبارت فوق را به صورت زیر بازنویسی می‌کنیم:

با داشتن $\theta^{(1)},...,\theta^{(n_u)}$ برای یادگیری $x^{(1)},...,x^{(n_m)}$ :

$$\begin{eqnarray} \min_{x^{(1)},x^{(2)},...,x^{(n_m)}} \frac{1}{2} \sum_{i=1}^{n_m} &\sum_{j:r(i,j)=1}& \left((\theta^{(j)})^Tx^{(i)}-y^{(i,j)}\right)^2 \\ &+&\frac{\lambda}{2}\sum_{i=1}^{n_m}\sum_{k=1}^{n}(x^{(i)}_{k})^2 \end{eqnarray}$$

در بخش قبلی یاد گرفتیم که چگونه با داشتن خصوصیات $x^{(1)},...,x^{(n_m)}$ و نمره هر فیلم پارامترهای $\theta^{(1)},...,\theta^{(n_u)}$ را تخمین بزنیم و در این بخش هم یاد گرفتیم که با داشتن $\theta^{(1)},...,\theta^{(n_u)}$ می‌توانیم خصوصیات $x^{(1)},...,x^{(n_m)}$ را یاد بگیریم. در حقیقت الان با مسئله‌ای مشابه تخم مرغ زودتر وجود داشته یا مرغ؟ مواجه هستیم. به عبارت دیگر کدام یک از این الگوریتم‌ها قبل از دیگری می‌آیند؟

کاری که باید انجام دهید این است که مقداری را برای $\theta$ حدس بزنید و بر اساس آن خصوصیت‌ها را محاسبه کنید. سپس از خصوصیت‌های به دست آمده دوباره جهت پیش‌بینی بهتر $\theta$ استفاده و $\theta$ را محاسبه کنید. در ادامه از $\theta$ های به دست آمده برای بهبود پیش‌بینی خصوصیت‌ها استفاده کنید و ... . این روند را اگر به اندازه کافی تکرار کنیم در آخر خصوصیت‌ها برای فیلم‌‌ها و پارامترهای $\theta$ برای کاربران به خوبی پیش‌بینی می‌شوند.

این اساس کار الگوریتم Collaborative Filtering یا همان فیلتر مشارکتی است ولی الگوریتم نهایی که از آن استفاده خواهیم کرد نیست. در ادامه این الگوریتم را بهبود می‌بخشیم و از لحاظ محاسباتی آن را بهینه می‌کنیم.

الگوریتم فیلتر کردن مشارکتی

دیدیم با داشتن $x^{(1)},...,x^{(n_m)}$ برای پیش‌بینی پارامترهای $\theta^{(1)},...,\theta^{(n_u)}$ باید:

$$\begin{eqnarray} \min_{\theta^{(1)},\theta^{(2)},...,\theta^{(n_u)}} \frac{1}{2} \sum_{j=1}^{n_u} &\sum_{i:r(i,j)=1}& \left((\theta^{(j)})^Tx^{(i)}-y^{(i,j)}\right)^2 \\ &+&\frac{\lambda}{2}\sum_{j=1}^{n_u}\sum_{k=1}^{n}(\theta^{(j)}_{k})^2 \end{eqnarray}$$

و با داشتن $\theta^{(1)},...,\theta^{(n_u)}$ برای تخمین خصوصیت‌های $x^{(1)},...,x^{(n_m)}$ باید:

تابع هزینه فیلتر کردن مشارکتی ترکیب دو مسئله بالا است و کاری که می‌خواهیم انجام دهیم به این صورت است که به صورت همزمان تابع هزینه زیر را نسبت به $x^{(1)},...,x^{(n_m)}$ و $\theta^{(1)},...,\theta^{(n_u)}$ کمینه کنیم.

$$\begin{eqnarray} J(x^{(1)},&.&..,x^{(n_m)},\theta^{(1)},...,\theta^{(n_u)}) = \\ &\frac{1}{2}& \sum_{(i,j):r(i,j)=1} \left((\theta^{(j)})^Tx^{(i)}-y^{(i,j)}\right)^2 \\ &+&\frac{\lambda}{2}\sum_{i=1}^{n_m}\sum_{k=1}^{n}(x^{(i)}_{k})^2 + \frac{\lambda}{2}\sum_{j=1}^{n_u}\sum_{k=1}^{n}(\theta^{(j)}_{k})^2 \end{eqnarray}$$

$$ \min_{\substack{x^{(1)},...,x^{(n_m)} \\ \theta^{(1)},...,\theta^{(n_u)}}} J(x^{(1)},...,x^{(n_m)},\theta^{(1)},...,\theta^{(n_u)}) $$

در این نسخه جدید به جای رفت و برگشت بین به دست‌اوردن $\theta$ و $$x$$ با استفاده از دو تابع هزینه، آنها را به صورت پارامتر به تابع هزینه جدید داده‌ایم و به صورت همزمان $\theta$ و $$x$$ را کمینه می‌کنیم.

آخرین نکته درباره این الگوریتم اینکه قرارداد $$x_0 = 1$$ را در اینجا به کار نمی‌بریم و $x \in \mathbb{R}^n$ و همچنین $\theta \in \mathbb{R}^n$ . دلیل این کار هم آن است که اگر الگوریتم به خصوصیتی نیاز داشته باشد که همواره یک باشد، می‌تواند خودش این را یاد بگیرد و به اصطلاح برنامه نویسی نیازی به سخت نویسی (hard code) آن نیست.

بنابراین الان می‌توانیم الگوریتم فیلتر کردن مشارکتی را به شکل زیر بنویسیم:

مقدار دهی اولیه به $x^{(1)},...,x^{(n_m)}$ و $\theta^{(1)},...,\theta^{(n_u)}$ با مقادیر تصادفی کوچک.
کمینه کردن $J(x^{(1)},...,x^{(n_m)},\theta^{(1)},...,\theta^{(n_u)})$ با استفاده از Gradeint Descent یا الگوریتم‌های پیشرفته کمینه کردن.
برای یک کاربر با پارامترهای $\theta$ و یک فیلم با خصوصیت‌های $$x$$ یاد گرفته شده، نمره فیلم را بر اساس $\theta^Tx$ پیش‌بینی کنید.

<< مبحث قبلی مبحث بعدی >>