Building an Anomaly Detection System
ساختن و ارزیابی یک سیستم یافتن بیهنجاری
در فصلهای قبل در مورد اهمیت ارزیابی الگوریتم توسط یک عدد حقیقی بحث کردیم و دیدیم که در هنگام ساختن یک الگوریتم یادگیری (انتخاب خصوصیتها و ...) اگر راهی برای ارزیابی الگوریتم خود داشته باشیم، تصمیمگیریها بسیار آسانتر خواهد شد.
در اینجا هم اگر بتوانیم عددی داشته باشیم که الگوریتم بافتن بیهنجاری را توسط آن ارزیابی کنیم، تصمیمگیریها در ساختن یک یادگیری مناسب جهت تشخیص بیهنجاری، برای ما بسیار آسانتر خواهد شد.
جهت ارزیابی یک سیستم یافتن بیهنجاری، فرض میکنیم که یک مجموعه داده برچسب گذاری شده به عنوان داده بیهنجار یا نرمال (\(y=0\) اگر داده نرمال باشد و \(y=1\) اگر داده بیهنجار باشد) داریم. به عبارتی با آن به مانند یک مسئله یادگیری با نظارت برخورد میکنیم. روند کار برای ساختن ابزاری جهت ارزیابی سیستم یافتن بیهنجاری به صورت زیر است:
- مجموعه دادههای بدون برچسب \(x^{(1)}, x^{(2)}, ...., x^{(m)}\) را از دادههای نرمال جهت مجموعه آموزش خود انتخاب میکنیم (البته گاهی ممکن است در انتخاب این دادهها به صورت تصادفی تعدادی داده بیهنجار هم وارد شود که در صورت کم بودن تعداد آنها مشکلی ایجاد نمیشود).
-
در این مرحله مجموعه دادههای cv و test را که در آنها داده بیهنجار هم وجود دارد تشکیل میدهیم.
$$ \text{cv set} = (x^{(1)}_{cv}, y^{(1)}_{cv}), ..., (x^{(m_{cv})}_{cv}, y^{(m_{cv})}_{cv})$$ $$ \text{test set} = (x^{(1)}_{test}, y^{(1)}_{test}), ..., (x^{(m_{test})}_{test}, y^{(m_{test})}_{test})$$
قبل از نوشتن الگوریتم برای روشن شدن این 2 مرحله مثال زیر را بررسی میکنیم:
فرض کنید در مثال ساختن موتور هواپیما، 10000 موتور خوب (داده نرمال) و 20 عدد دارای مشکل (داده بیهنجار) داریم. از این مجموعه داده معمولا به شکل زیر مجموعه دادههای آموزش، cv و test را انتخاب میکنیم.
$$\text{training set} = 6000 \quad \text{good engines} \quad (y = 0)$$
$$\text{cv set} = 2000 \quad (y = 0), 10 \quad \text{anomalous} \quad (y=1)$$
$$\text{training set} = 2000 \quad (y = 0), 10 \quad (y=1)$$
این نوع تقسیمبندی؛ یعنی (%60, %20, %20) بهترین نوع تقسیمبندی دادهها به سه دسته مورد نظر است.
بعد از انجام دو مرحله گفته شده، میتوان الگوریتم مربوط به ارزیابی را به شکل زیر بنویسیم:
- \(p(x)\) را برای مجموعه دادههای \(\{x^{(1)},x^{(2)},...,x^{(m)}\}\) محاسبه کنید.
-
روی مجموعه دادههای cv و test پیشبینی کنید که:
$$y= \begin{cases} 1 \quad \text{if} \quad p(x)\lt \epsilon \quad (\text{anomaly})\\ 0 \quad \text{if} \quad p(x)\ge \epsilon \quad (\text{normal}) \end{cases} $$
سنجشهای ممکن برای برای ارزیابی میتواند یکی از موارد زیر باشد:
- true positive, false positive, false negative, true negative
- precision/recall
- F1-score
یکی از راههای انتخاب \(\epsilon\) میتواند استفاده از مجموعه داده cv باشد. به این صورت که برای مقادیر مختلف \(\epsilon\) کار را انجام دهیم و هر کدام که F1-score را بیشینه کرد به عنوان مقدار \(\epsilon\) انتخاب کنیم.
توجه داشته باشید که دادههای ما به شدت skewed هستند (دادههای نرمال ما بسیار بیشتر از دادههای بیهنجار است). در چنین مواردی classification accuracy سنجش خوبی نخواهد بود و به جای آن میتوان از موارد اشاره شده در بالا استفاده کرد.
یافتن بیهنجاری در مقایسه با یادگیری با نظارت
سوالی که ممکن است پیش آید این است که اگر تعدادی داده بیهنجار و تعدادی داده نرمال داریم چرا به جای یافتن بیهنجاری از یادگیری با نظارت استفاده نکنیم؟ هدف ما در این بخش پاسخ به این سوال است.
ابتدا بهتر است که خصوصیات دادههای یادگیری با نظارت و یافتن بیهنجاری را با هم مقایسه کنیم.
در یادگیری با نظارت:
- تعداد هر دو نوع داده مثبت و منفی زیاد است.
- در این نوع مسائل به اندازه کافی داده مثبت وجود دارد که الگوریتم یاد بگیرد مثالهای مثبت آینده چه شکلی هستند.
- به احتمال زیاد مثالهای مثبت آینده هم مشابه همانها هستند که در داده آموزش وجود دارند.
اما در در یافتن بیهنجاری:
- تعداد دادههای مثبت \((y=1)\) بسیار کم است (معمولا بین ۰ تا ۲۰).
- تعداد دادههای منفی \((y=0)\) بسیار زیاد است.
- دادههای مثبت را تنها برای مجموعههای cv و test استفاده میکنیم.
- در دادههای آموزش تنها از دادههای منفی برای ساختن مدل احتمالاتی \(p(x)\) استفاده میکنیم.
- تعداد انواع بیهنجاری بسیار زیاد است و برای هر الگوریتمی بسیار سخت خواهد بود که از مثالهای مثبت یاد بگیرد که بیهنجاریها چه شکلی هستند.
- ممکن است بیهنجاریهای آینده هیچ شباهتی به بیهنجاریهای قبلی نداشته باشند.
بنابراین در این موارد بهتر است به جای اینکه به سختی تلاش کنیم تا بیهنجاریها را پیشبینی کنیم، عاقلانهتر آن است که دادههای منفی را بر اساس توزیع گاوسین بررسی کنیم.
البته دقت داشته باشید که در مسائلی مانند ایمیل اسپم، هر چند تعداد انواع اسپم بسیار زیاد است ولی از هر نوع آن به اندازه کافی مثال داریم که آن را جز مسائل یادگیری با نظارت قرار دهیم.
در جدول زیر برخی از موارد کاربرد یادگیری با نظارت در برابر یافتن بیهنجاری آورده شده است:
| یافتن بیهنجاری | یادگیری با نظارت |
|---|---|
| یافتن کلاهبرداری | طبقهبندی اسپم برای ایمیل |
| تولید (ساختن) موتور هواپیما | پیشبینی آب و هوا (بارانی، آفتابی) |
| رسد کامپوترها در یک مرکز داده | طبقهبندی سرطان |
در هر یک از موارد کاربرد یافتن بیهنجاری در صورتی که تعداد مثالهای مثبت زیاد باشند، میتوان آن مورد را به یادگیری با نظارت شیفت داد.
از چه خصوصیاتی استفاده کنیم؟
انتخاب خصوصیتها برای الگوریتم یافتن بیهنجاری تاثیر بسیار زیادی در عملکرد آن دارد. به همین جهت در این بخش میخواهیم چند توصیه و راهنمایی جهت انتخاب خصوصیتهای مناسب برای الگوریتم بیهنجاری را بیان کنیم.
یکی از فرضهایی که برای خصوصیت الگوریتم یافتن بیهنجاری در نظر گرفتیم، توزیع گاوسین این خصوصیتها بود. میتوان با رسم هیستوگرام مربوط به خصوصیت از نحوه توزیع آن مطلع شد که آیا گاوسین است یا خیر؟ هر چند که اگر توزیع به صورت گاوسین هم نباشد مشکلی ایجاد نمیکند ولی بهتر است که بوسیله یک سری تبدیلات ریاضی در صورت امکان توزیع آن را به صورت گاوسی به الگوریتم بدهیم.
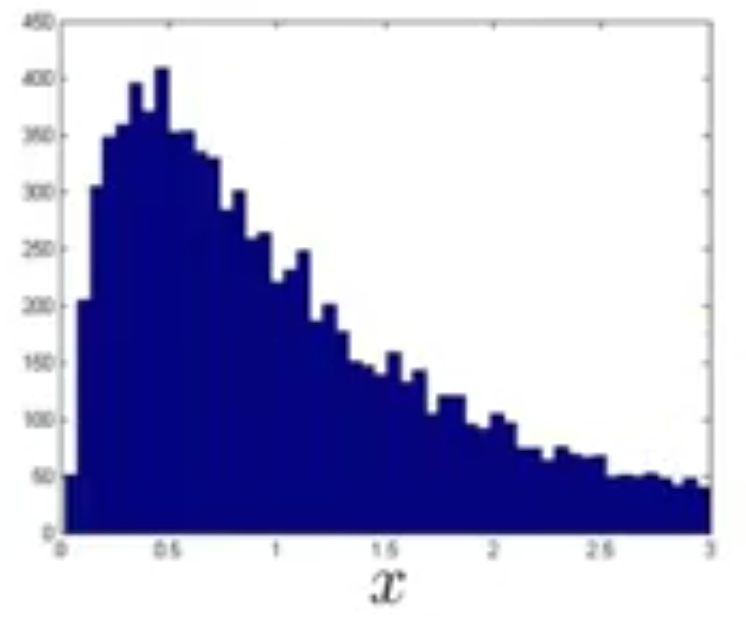
برای روشن شدن موضوع مثلا فرض کنید توزیع خصوصیت \(x\) به شکل زیر باشد:
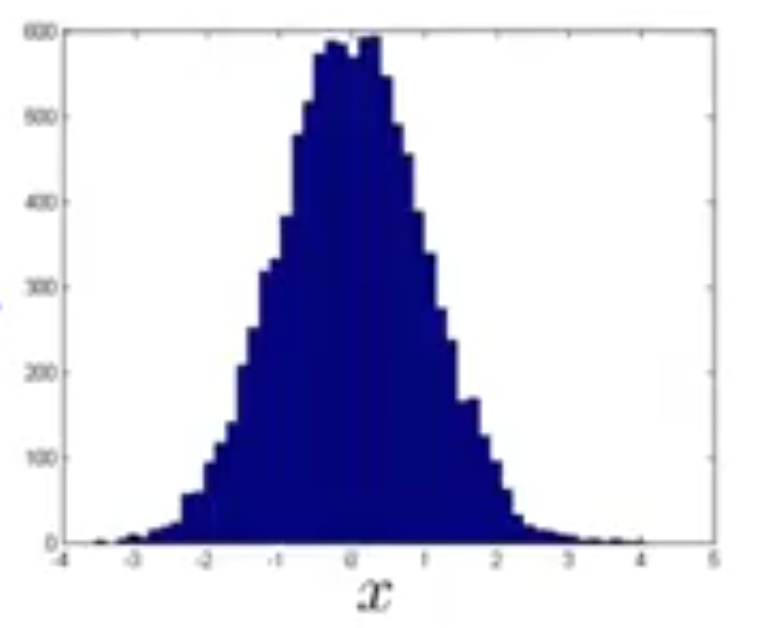
که هیچ شباهتی به توزیع گاوسین ندارد ولی در این مورد خاص اگر \(\log(x)\) را رسم کنیم، مشاهده میکنیم که توزیع آن به مانند شکل زیر و گاوسین خواهد شد و میتوانیم از \(\log(x)\) به جای خود خصوصیت \(x\) استفاده کنیم.
به صورت کلی یکی از تبدیلاتی که میتوان روی خصوصیتها انجام داد تا شاید توزیع آنها به صورت نرمال درآید تبدیل \(\log(x+c)\) است که در آن \(c\) یک ثابت است.
دیگر تبدیل رایج استفاده از یک عبارت نمایی است. مثلا به جای خصوصیت \(x\) از \(\sqrt{x}\) یا همان \(x^{\frac{1}{2}}\) استفاده کرد. در صورت نیاز میتوان توان \(x\) را تغییر داد تا توزیع آن به توزیع گاوسین نزدیکتر شود.
بنابراین به صورت خلاصه میتوان گفت که هرچند اگر خصوصیت \(x\) به صورت گاوسین هم توزیع نشده باشد معمولا اشکالی در الگوریتم ایجاد نمیکند، ولی بهتر است که در صورت امکان با انجام تبدیلاتی مشابه آنچه که بیان شد، یک خصوصیت جدید با توزیع گاوسین را ایجاد و به جای خصوصیت اصلی آن را به الگورینتم یافتن بیهنجاری بدهیم.
تحلیل خطا برای یافتن الگوریتم یافتن بیهنجاری
در ساختن مدل \(p(x)\) برای الگوریتم یافتن بیهنجاری معمولا امیدواریم که \(p(x)\) برای نمونههای نرمال \(x\) مقداری بالا و برای نمونههای بیهنجار مقداری کوچک داشته باشد.
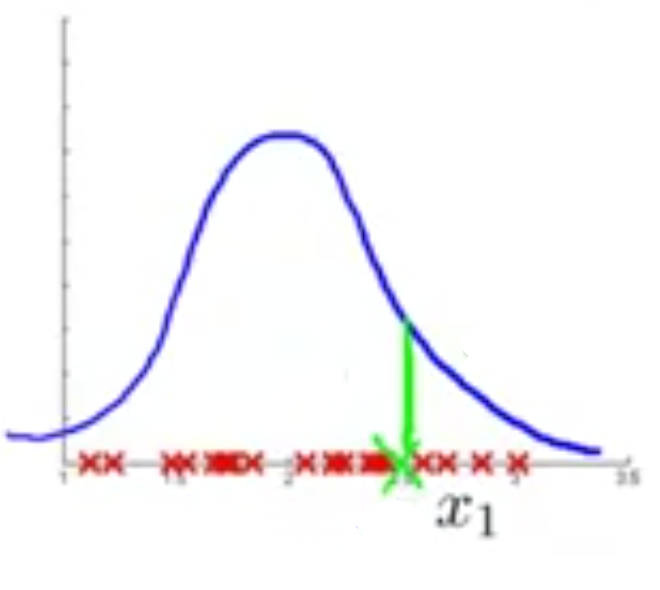
مشکل رایجی که وجود دارد این است که \(p(x)\) ممکن است مقداری بدهد که برای هر دو نمونه نرمال و بیهنجار قابل مقایسه باشد (مثلا هر دو بزرگ). برای درک بهتر موضوع به شکل زیر نگاه کنید، ضربدر سبز رنگ مشخص شده روی نمودار نمونه بیهنجار است ولی چنانکه ملاحظه میکنید در بین نمونههای نرمال قرار گرفته و نسبتا دارای مقدار احتمال بالایی است (ارتفاع خط سبز رنگ).
در چنین مواقعی بهترین کار آن است که به نمونه نگاه کنیم، مثلا در مورد ساختن متور هواپیما، موتور را بررسی کنیم و ببینیم که چه چیزی برای آن مشکل ایجاد کرده است که جزء نمونههای بیهنجار قرار گرفته است و بر اساس آن یک خصوصیت جدید برای الگوریتم تعریف کنیم که بتواند این نمونه بیهنجار را هم تشخیص دهد.
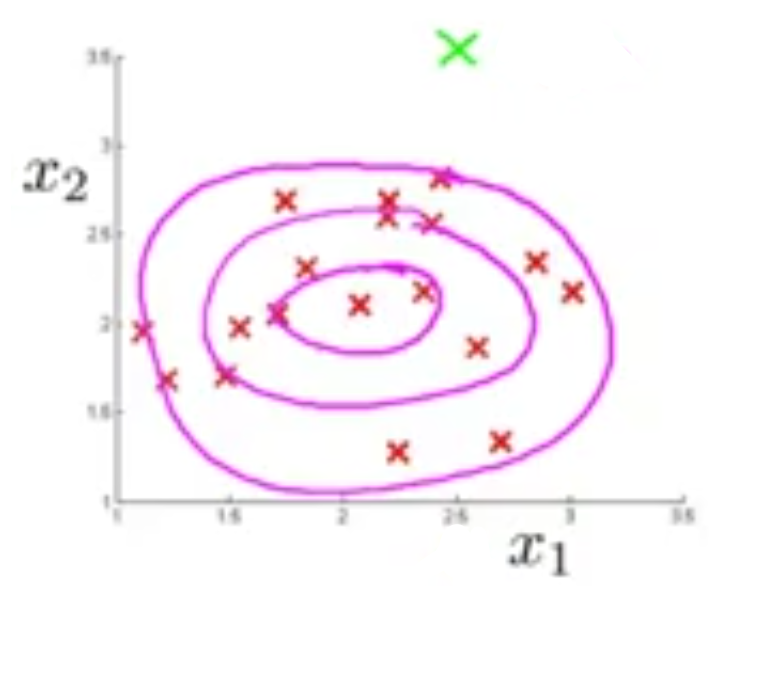
در این حالت مشاهده میکنید که ضربدر سبزرنگ هر چند از دید خصوصیت \(x_1\) مقدار نرمالی دارد ولی مقدار \(x_2\) برای آن نسبت به نمونههای دیگر بسیار بالاتر است و میتوان ان را به عنوان نمونه بیهنجار شناسایی کرد.
به عنوان آخرین نکته در مورد انتخاب خصوصیتها، همواره سعی کنید خصوصیتهایی را انتخاب کنید که ممکن است مقادیر بسیار زیاد یا بسیار کمی در هنگام بیهنجاری داشته باشند. به عنوان مثال در رصد کردن دادهّا در یک مرکز داده میتوانید خصوصیتهای زیر را انتخاب کنید.
استفاده از حافظه توسط کامپیوتر \(x_1 =\)
تعداد دسترسی به دیسکها بر ثانیه \(x_2 =\)
بار \(x_3 = CPU\)
ترافیک شبکه \(x_4 =\)
حال فرض کنید که بارگذاری CPU و ترافیک شبکه به صورت خطی با هم افزایش پیدا میکنند که فرض منطقیای هم به نظر میرسد. حال فرض کنید چندین سرور داریم و کاربران زیادی در حال استفاده از یکی از سرورها هستند. بنابراین ترافیک روی سرور و بار CPU آن زیاد خواهد بود. اما حالا فرض کنید که یکی از کدهای ما باعث میشود که کامپیوتر در یک لوپ بینهایت گیر کند (کد دارای اشکال باشد) در چنین حالتی در حالیکه بار CPU در حال افزایش است ترافیک شبکه ثابت خواهد ماند. در نتیجه برای یافتن چنین بیهنجاری بهتر است خصوصیت جدیدی را به صورت
یا
تعریف کنیم. بنابراین با شک کردن در اینکه چه نوع بیهنجاری میتواند برای سیستم ما پیش بیاید، میتوان خصوصیتهای جدیدی را برای یافتن آن نوع بیهنجاری تعریف کرد.