Bias vs. Variance

سوگیری در برابر تغییرات

بیشتر اوقات دلیل کار نکردن فرضیه به دست آمده به یکی از دو دلیل زیر است:

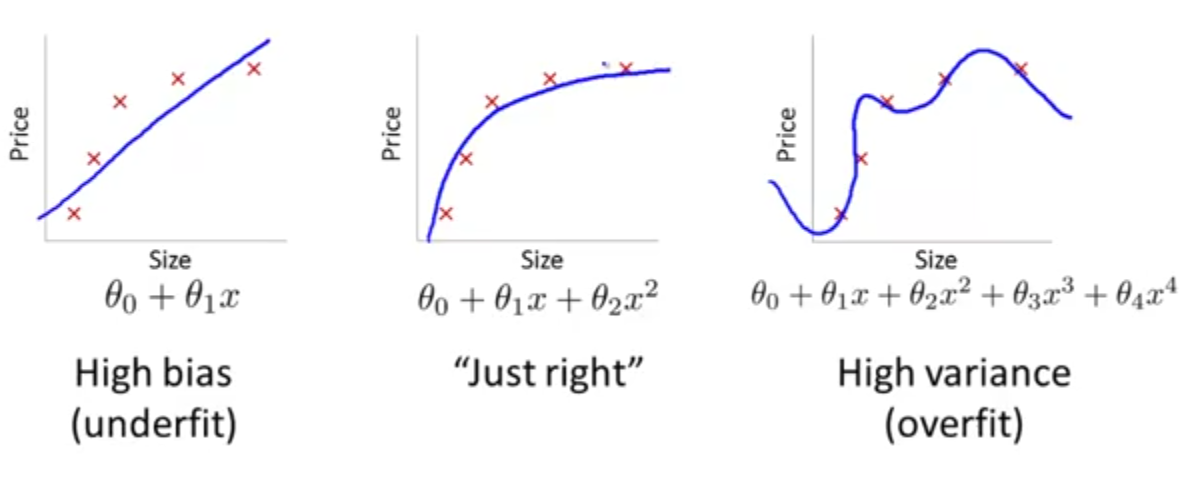
underfitting $\rightarrow$ High Bias
overfitting $\rightarrow$ High Variance

اگر بتوانیم تشخیص دهیم که الگوریتم ما از کدامیک از موارد بالا رنج می‌برد، می‌توانیم عملکرد کلی الگوریتم را تا حد زیادی بهبود ببخشیم. ولی سوال این است که از کجا بفهمیم فرضیه ما از کدامیک رنج می‌برد؟

در بخش قبلی خطای آموزش و خطای اعتبارسنجی را به صورت زیر تعریف کردیم:

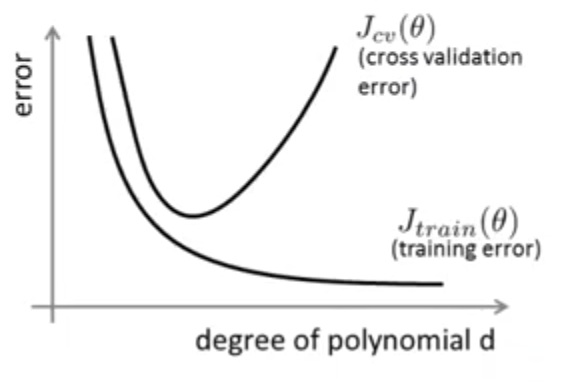
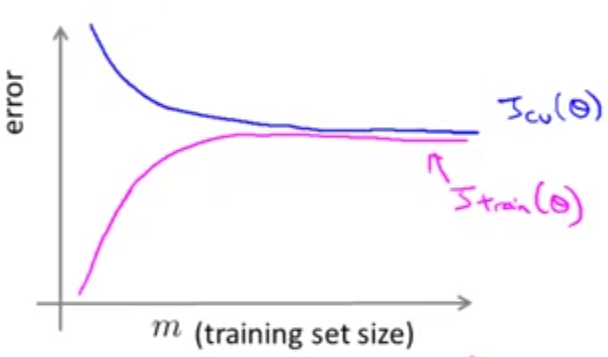
$$ J_{training}(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h_{\theta}(x^{(i)}) - y^{(i)})^2 $$ $$ J_{cv}(\theta) = \frac{1}{2m_{cv}} \sum_{i=1}^{m_{cv}} (h_{\theta}(x^{(i)}_{cv}) - y^{(i)}_{cv})^2 $$

اگر مقدار این دو خطا را برحسب درجه چند جمله‌ای رسم کنیم، نموداری شبیه شکل زیر خواهیم داشت:

با دقت در این نمودار متوجه می‌شویم زمانی که درجه چند جمله‌ای کم است (underfitting) خطای آموزش زیاد و خطای اعتبارسنجی هم تقریبا برابر (یا کمی بیشتر) از آن است، به عبارتی دیگر هر دو دارای خطای بزرگی هستند. با افزایش درجه چند جمله‌ای خطای هر دو کاهش می‌یابد تا زمانیکه وارد محدوده مشکل overfitting می‌شویم. در این محدوده چون تابع فرضیه ما به خوبی داده‌های آموزش را برازش می‌کند، خطای آموزش کم است ولی در همین محدوده مشاهده می‌کنیم که خطای اعتبارسنجی زیاد و بسیار بیشتر از خطای آموزش است.

پس به صورت خلاطه می‌توان گفت برای تشخیص اینکه تابع فرضیه ما از کدام مورد رنج می‌برد، به صورت زیر می‌توان عمل کرد:

در مورد مشکل High Bias یا همان Underfitting داریم:

$$ J_{\text{train}}(\theta) \text{ will be high} $$ $$ J_{\text{cv}}(\theta) \approx J_{\text{train}}(\theta) $$

و برای مشکل High variance یا همان overfitting داریم:

$$ J_{\text{train}}(\theta) \text{ will be low} $$ $$ J_{\text{cv}}(\theta) \gg J_{\text{train}}(\theta) $$

اگر به جای

J_{cv}(\theta)

از

J_{test}(\theta)

استفاده کنیم، نتیجه مشابهی به دست خواهیم آورد.

منظم سازی و سوگیری/واریانس

در فصل‌های قبل مشاهده کردیم که منظم‌سازی می‌تواند از مشکل overfitting جلوگیری کند. اما چگونه بر سوگیری یا واریانس یک الگوریتم یادگیری تاثیر می‌گذارد؟

فرض کنید مدلی مانند مدل زیر داریم:

$$ h_{\theta}(x) = \theta_0 + \theta_1x + \theta_2x^2 + \theta_3x^3 + \theta_4x^4 $$

و جهت جلوگیری از overfitting می‌خواهیم از منظم‌سازی استفاده کنیم:

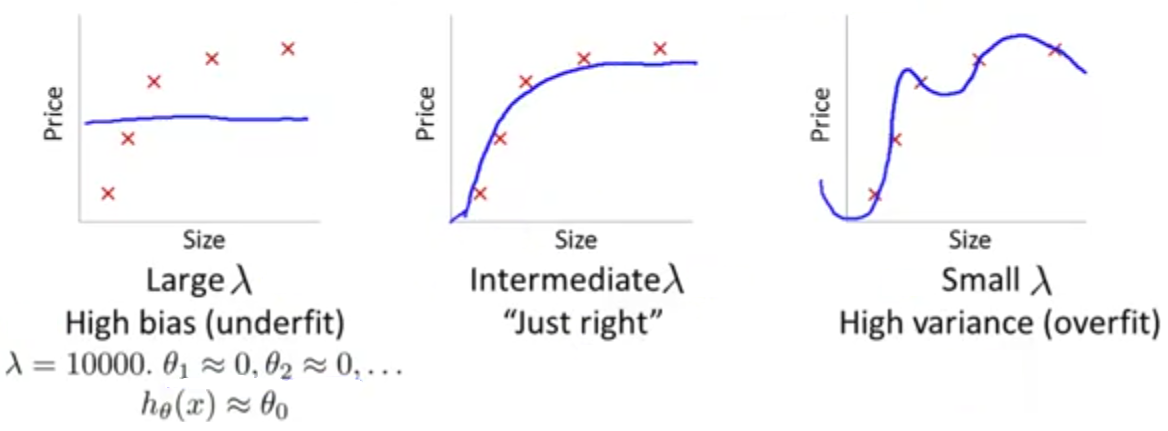
$$\begin{eqnarray} J(\theta) &=&\frac{1}{2m} \sum_{i=1}^{m} \left(h_{\theta}(x^{(i)}) - y^{(i)}\right)^2\\ &\quad& \quad \quad \quad + \frac{\lambda}{2m} \sum_{j=1}^{n} \theta^{2}_{j} \end{eqnarray}$$

چنانکه ملاحظه می‌کنید، در صورتی که مقدار $\lambda$ عددی بزرگی باشد، مشکل (High Bias) یا Underfitting رخ می‌دهد. همچنین اگر مقدار $\lambda$ عدد کوچکی باشد، با مشکل (High variance) یا overfitting مواجه خواهیم شد و فقط به ازای یک مقدار حد وسط $\lambda$ است که جواب قابل قبولی خواهیم داشت. در این بخش می‌خواهیم در مورد چگونگی انتخاب پارامتر منظم‌سازی یا همان $\lambda$ به صورت خودکار بحث کنیم.

خطاهی آموزش، اعتبارسنجی و آزمایش را به مانند قبل و بدون در نظر گرفتن جمله منظم‌سازی فرض می‌کنیم:

$$ J_{training}(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h_{\theta}(x^{(i)}) - y^{(i)})^2 $$ $$ J_{cv}(\theta) = \frac{1}{2m_{cv}} \sum_{i=1}^{m_{cv}} (h_{\theta}(x^{(i)}_{cv}) - y^{(i)}_{cv})^2 $$ $$ J_{test}(\theta) = \frac{1}{2m_{test}} \sum_{i=1}^{m_{test}} (h_{\theta}(x^{(i)}_{test}) - y^{(i)}_{test})^2 $$

کاری که باید انجام دهیم این است که به ازای لامداهای مختلف تابع فرضیه را محاسبه و سپس بر اساس پارمترهای به دست آمده $J_{cv}$ها را محاسبه کنیم. با انتخاب کمترین مقدار به دست آمده به عنوان مدل، آن را روی $J_{test}$ آزمایش می‌کنیم تا ببینیم مدل انتخاب شده چقدر خوب عمل می‌کند.

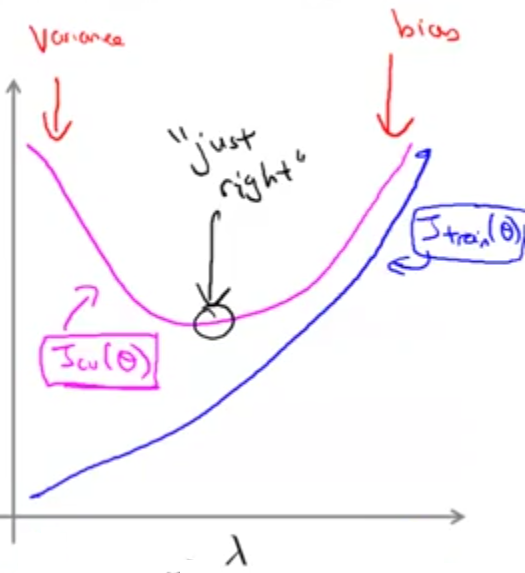
$$ 1. \text{Try } \lambda = 0 \rightarrow J(\theta) \rightarrow \theta^{(1)} \rightarrow J_{cv}(\theta^{(1)}) $$ $$ 2. \text{Try } \lambda = 0.01 \rightarrow J(\theta) \rightarrow \theta^{(2)} \rightarrow J_{cv}(\theta^{(2)}) $$ $$ 3. \text{Try } \lambda = 0.02 \rightarrow J(\theta) \rightarrow \theta^{(3)} \rightarrow J_{cv}(\theta^{(3)}) $$ $$ 4. \text{Try } \lambda = 0.04 \rightarrow J(\theta) \rightarrow \theta^{(4)} \rightarrow J_{cv}(\theta^{(4)}) $$ $$ 5. \text{Try } \lambda = 0.08 \rightarrow J(\theta) \rightarrow \theta^{(5)} \rightarrow J_{cv}(\theta^{(5)}) $$ $$ \vdots $$ $$ 10. \text{Try } \lambda = 10 \rightarrow J(\theta) \rightarrow \theta^{(10)} \rightarrow J_{cv}(\theta^{(10)}) $$

در اینجا لامدا را با ضریب ۲ افزایش داده‌ایم. مقادیر لامدا می‌توانند کمتر و یا بیشتر از این مقادیر انتخاب شوند.

اگر خطای آموزش و خطای اعتبارسنجی را بر حسب لامدا رسم کنیم به نموداری شبیه شکل زیر می‌رسیم:

با دقت در نمودار مشاهده می‌کنیم که به ازای لامداهای کوچک خطای آموزش کم و خطای اعتبارسنجی زیاد است به عبارتی با مشکل overfitting مواجه هستیم و همچنین به ازای لامداهای بزرگ هر دوی خطای آموزش و خطای اعتبارسنجی بزرگ هستند و به عبارت دیگر با مشکل underfitting مواجه هستیم. دایره مشکی رنگ مشخص شده روی منحنی خطای اعتبارسنجی جایی است که بهترین مقدار لامدا را داریم. یعنی حدودا جایی که منحنی خطای اعتبارسنجی کمترین مقدار خود را دارد.

منحنی‌های یادگیری

منحنی یادگیری اغلب چیز مفیدی جهت رسم است. از روی آن می‌توانید چک کنید که الگوریتم شما به درستی کار می‌کند و یا عملکرد الگوریتم خود را بر اساس آن بهبود ببخشید. همچنین ابزاری بسیار سودمند در زمینه پی بردن به اینکه الگوریتم ما از مشکل سوگیری یا واریانس رنج می‌برد است.

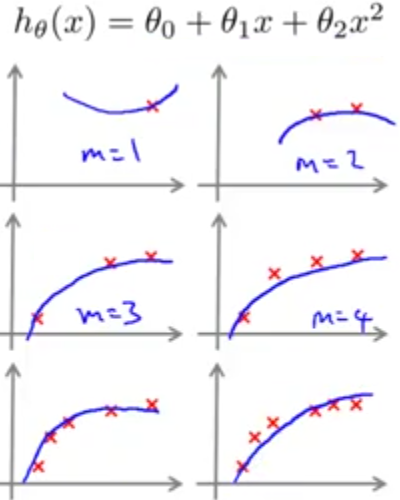
منحنی یادگیری به صورت رسم منحنی‌های خطای آموزش و خطای اعتبارسنجی (یا خطای آزمایش) نسبت به تعداد داده‌ها است. برای مثال فرض کنید مانند شکل زیر یک تابع درجه دوم را به داده‌هایی که به صورت مصنوعی تعداد آنها کم شده‌اند (خودمان تعداد داده‌ها را کم کرده‌ایم) برازش می‌دهیم. زمانی که تنها یک داده داریم، مدل ما به خوبی این داده را برازش می‌کند و خطای آموزش صفر خواهد بود و این روند شاید تا زمانیکه به ۳ داده برسیم هم ادامه یابد ولی با فزایش بیشتر تعداد داده‌ها دیگر مدل درجه دوم ما قادر نخواهد بود که همه داده‌ها را برازش کند و خطای آموزش به تدریج با افزایش تعداد داده‌ها افزایش می‌یابد.

از طرفی زمانی که تنها از روی یک داده تابع فرضیه خود را به دست آورده‌ایم، قطعا نمی‌تواند عمومیت خوبی داشته باشد و خطای اعتبارسنجی ما زیاد خواهد بود. اما به تدریج که تعداد داده‌ها افزایش پیدا می‌کند، تابع فرضیه به دست آمده می‌تواند بهتر به داده‌های جدید تعمیم پیدا کند و در نتیجه خطای اعتبارسنجی با افزایش تعداد داده‌ها کاهش می‌یابد. در نهایت منحنی شبیه به نمودار زیر خواهیم داشت:

حال می‌خواهیم ببینیم که این منحنی یادگیری در زمانیکه با مشکل High Bias مواجه هستیم چگونه خواهد بود؟

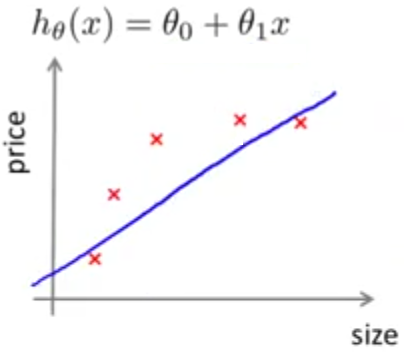
برای این منظور چنانکه در شکل زیر نشان داده شده است، یک تابع خطی را به مجموعه داده‌هایمان که شامل 5 نقطه است براش داده‌ایم. واضح است که یک تابع خطی نمی‌تواند همه نقاط را برازش کند و خطای آموزش ما مقداری غیر صفر خواهد بود.

حال اگر تعداد داده‌هایمان را افزایش دهیم، مشاهده می‌کنیم که تقربا همان خطی که در مرحله قبل داشتیم را به دست می‌اوریم و تابع فرضیه ما تفاوت چندانی نمی‌کند. در حقیقت تابع خطی ما توانایی برازش داده‌هایمان را ندارد و اگر کلی داده دیگر هم اضافه کنیم تغییر خاصی اتفاق نمی‌افتد.

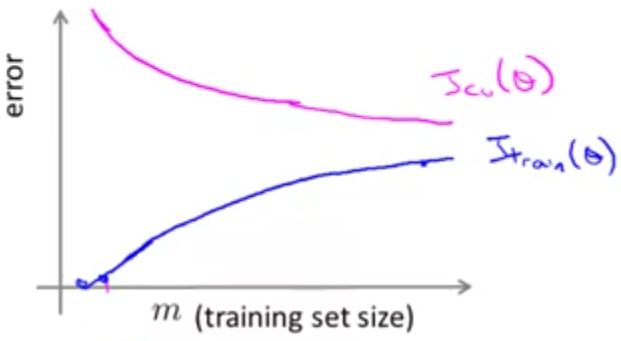
اگر منحنی‌ خطای اعتبارسنجی را برای این مثال رسم کنیم، مشاهده خواهیم کرد که در ابتدا خطا بسیار زیاد است. در ادامه این خطا با افزایش تعداد داده‌ها کاهش می‌یابد ولی خیلی زود به جایی می‌رسد که دیگر توانایی بهتر شدن را ندارد و ادامه منحنی تقریبا به صورت یک خط راست در می‌آید. اگر منحنی خطای آموزش را هم رسم کنیم، مشاهده خواهیم کرد که در ابتدا که تعداد داده‌های ما کم است این خطا هم کم ولی در ادامه با افزایش تعداد داده‌ها خطای آموزش هم بیشتر می‌شود. به عبارت دیگر از آنجا که تعداد پارامترهای ما بسیار کمتر از تعداد داده‌هایمان است، مدل ما نمی‌تواند داده‌ها را به خوبی برازش کند و در نتیجه خطای آموزش و خطای اعتبارسنجی هر دو زیاد و نزدیک به هم خواهند بود و منحنی یادگیری مانند شکل زیر خواهد بود:

پس مشکل High Bias در بالا بودن هر دوی خطای آموزش و خطای اعتبارسنجی منعکس است و در اینجا به نکته جالبی می‌رسیم که اگر فرضیه ما دچار مشکل High Bias باشد، تنها افزایش دادن تعداد داده‌های آموزش به هیچ عنوان برای ما کارگشا نخواهد بود و لازم نیست بیخودی روی این مسئله وقت بگذاریم.

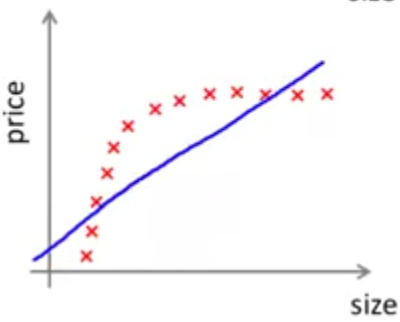
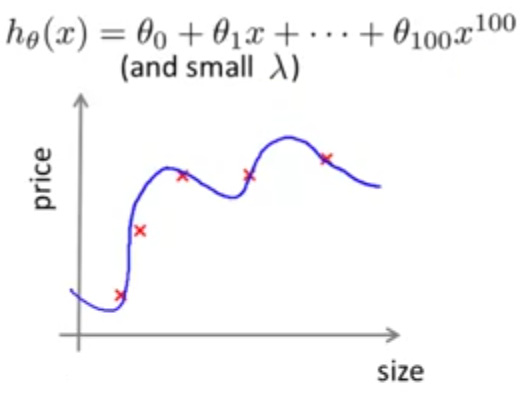
اما اگر مدل ما یک چند جمله‌ای مرتبه بالا (مثلا مرتبه 100) باشد، زمانیکه تعداد داده‌هایمان کم است بسیار خوب آنها را برازش و خطای آموزش بسیار کم خواهد بود.

با افزایش تعداد داده‌ها در حالیکه خطای آموزش مقداری افزایش می‌یابد ولی همچنان این مدل داده‌ها را نسبتا خوب برازش می‌کند و خطای آموزش خیلی زیاد نمی‌شود.

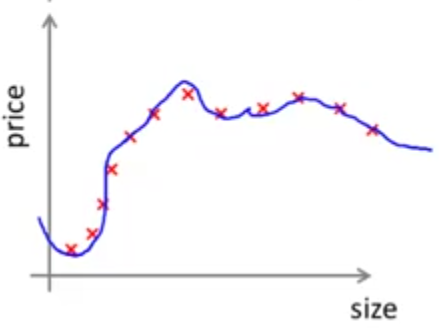
در مورد خطای اعتبارسنجی هم می‌توان گفت که در ابتدا به دلیل کم بودن تعداد داده‌ها فرضیه به دست آمده عمومیت خوبی ندارد و خطای اعتبارسنجی زیاد است. در ادامه با فزایش تعداد داده‌ها هر چند خطای اعتبارسنجی کاهش می‌یابد ولی کماکان مقدار آن زیاد است و چنانکه در شکل زیر مشاهده می‌کنید شکافی که بین خطای اعتبارسنجی و خطای آموزش وجود دارد نشانگر وجود مشکل High Variance است.

در چنین حالتی به احتمال زیاد با فراهم کردن تعداد داده بیشتر برای مجموعه آموزش بتوانیم نتیجه بهتری کسب کنیم و با رسم نموداری شبیه به نمودار بالا مشاهده کنیم که خطای اعتبارسنجی کاهش و خطای آموزش افزایش می‌یابند به طوریکه شکاف بین آنها بسیار کم خواهد شد.

توجه داشته باشید که منحنی‌های یادگیری رسم شده در اینجا بسیار ایده‌آل هستند. در واقعیت ممکن است چنین منحنی‌های تر و تمیزی به دست نیاید. ولی اغلب اوقات منحنی‌های یادگیری رسم شده به گونه‌ای هستند که می‌توان از روی آنها در صورت وجود مشکل High Bias یا High Variance در الگوریتم، آن را متوجه شد.

تصمیم‌گیری برای گام بعدی

فرض کنید رگرسیون خطی منظم‌سازی شده را برای پیش‌بینی قیمت خانه‌ها به کار برده‌اید. با این حال هنگامیکه فرضیه خود را روی خانه‌های جدید اعمال می‌کنید، خطای بزرگ غیرقابل قبولی دارید. در گام بعدی چه کاری باید انجام دهید؟

فراهم کردن نمونه‌های آموزش بیشتر
استفاده از مجموعه کوچکتری از خصوصیت‌ها
فراهم کردن خصوصیت‌های بیشتر
اضافه کردن خصوصیت‌های چند جمله‌ای $(x_{1}^{2},x_{2}^{2},x_1x_2,etc)$
استفاده از لامدای کوچکتر
استفاده از لامدای بزرگتر

در صورتی که با استفاده از منحنی یادگیری یا به هر طریق دیگری فهمیدید که الگوریتم شما از مشکل High Variance رنج می‌برد، می‌توانید از موارد شماره 1، 2 و 6 استفاده کنید و اگر هم متوجه شدید که با مشکل High Bias مواجه هستید، می‌توانید از موارد شماره 3، 4 و 5 استفاده کنید. البته به یاد داشته باشید فراهم کردن خصوصیت بیشتر نه همیشه ولی معمولا می‌تواند مشکل High Bias را رفع کند.

شبکه‌های عصبی و overfitting

در قسمت پایانی این بخش می‌خواهیم همه آنچه را که تا اینجا یاد گرفته‌ایم به شبکه‌های عصبی ارتباط دهیم و ببینیم معماری یا نحوه ارتباط شبکه عصبی را چگونه انتخاب کنیم.

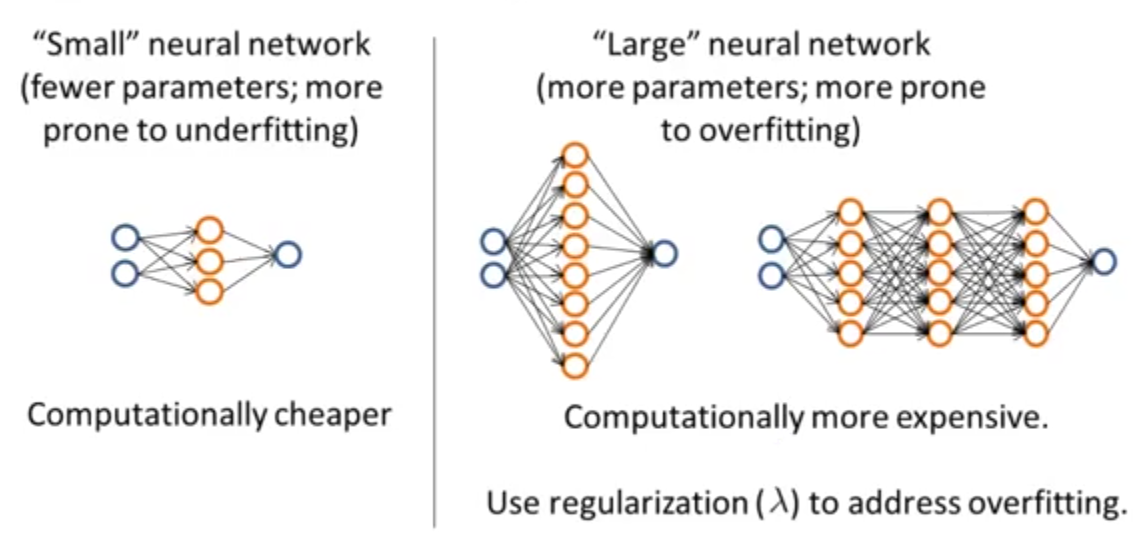
چنانکه به صورت خلاصه در شکل زیر هم نمایش داده شده است، در صورتیکه یک شبکه عصبی کوچک را انتخاب کنیم، ممکن است با مشکل underfitting مواجه شویم ولی مزیت اصلی آن در به صرفه بودن محاسبات است. از طرف دیگر اگر از شبکه عصبی بزرگتری استفاده کنیم با دو مشکل روبه‌رو خواهیم بود، اول اینکه محاسبات بیشتری باید انجام شود و دوم و مهمتر آنکه ممکن است الگوریتم دچار پدیده overfitting شود. به همین علت در این حالت بهتر است از منظم‌سازی استفاده شود. در نهایت استفاده از شبکه عصبی بزرگتر همراه با منظم‌سازی معمولا نتایج بهتری نسبت به یک شبکه عصبی کوچک ارائه می‌دهد.

اما جهت تعیین تعداد لایه‌ها و اینکه می‌خواهیم از چند لایه استفاده کنیم، یکی از روش‌ها می‌تواند تقسیم مجموعه داده‌ها به سه دسته آموزش، اعتبارسنجی و آزمایش باشد. سپس به همان روشی که پیشتر بحث شد، بعد از محاسبه پارامترها، $J_{cv}(\theta)$ را محاسبه و بعد از انتخاب مدل بر اساس آن، جواب‌ها را بوسیله $J_{test}(\theta)$ بسنجیم.

<< مبحث قبلی مبحث بعدی >>