Applying PCA

بازسازی از داده‌های فشرده شده

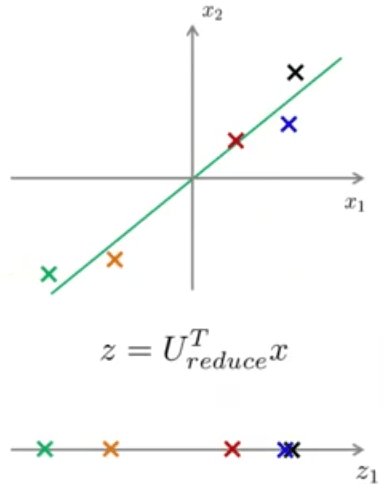
چنانکه دیدیم الگوریتم PCA یک الگوریتم فشرده سازی داده است و با استفاده از آن می‌توان برای مثال داده‌های 3 بعدی را به 2 بعدی کاهش داد. حال دنبال راهی هستیم که بتوانیم در صورت نیاز از داده‌های فشرده‌سازی شده به داده‌های اصلی برگردیم. به مثال زیر توجه کنید:

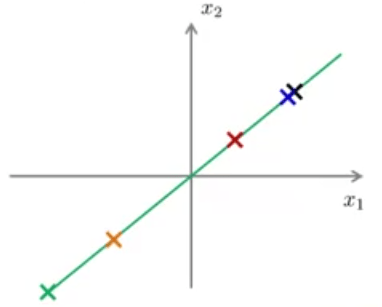
کاری که در بخش قبل انجام دادیم، محاسبه $$z$$ و انتقال داده‌ها از 2 بعد به یک بعد بود. در اینجا می‌خواهیم عکس این کار را انجام دهیم و از $z \in \mathbb{R}$ داده‌های اصلی یعنی $x \in \mathbb{R}^2$ را بازسازی کنیم. برای بازسازی داده‌های اصلی از داده‌های فشرده‌سازی شده می‌توان نوشت:

$$ x_{\text{approx}} = U_{\text{reduce}}.z $$

دلیل زیروند approx برای $$x$$ آن است که نمی‌توانیم دقیقا داده‌های اصلی را بازسازی کنیم ولی با تقریب خوبی می‌توان آن‌ها را به‌ دست‌آورد (به شرط آنکه خطای تصویرسازی زیاد نباشد).

انتخاب k

همانطور که در الگوریتم PCA گفتیم، بعد از محاسبه ماتریس کوواریانس و به دست آوردن ویژه بردارهای آن، تنها $$k$$ بردار اول را نیاز داریم. در این بخش می‌خواهیم در مورد نحوه انتخاب $$k$$ بحث کنیم.

یکی از راه‌های انتخاب $$k$$ استفاده از فرمول زیر است:

$$ \frac{\frac{1}{m}\sum_{i=1}^{m} {\lVert x^{(i)} - x^{(i)}_{\text{approx}} \rVert}^2}{\frac{1}{m} \sum_{i=1}^{m} {\lVert x^{(i)}\rVert}^2} \le 0.01 $$

که صورت کسر فوق میانگین مربعات خطای تصویر کردن و مخرج آن تغییرات کل در داده است.

اگر از زبان PCA برای بیان فرمول بالا استفاده کنیم معمولا گفته می‌شود که %99 تغییرات حفظ شده است (99% of variance is retained). اما نگران مفهوم این عبارت نباشید و فقط کافی است بدانید که اگر کسی این عبارت را به کار برد منظورش آن است که کسر معرفی شده در بالا کوچکتر مساوی 0.01 است. اعداد دیگری هم به‌جای 0.01 رایج هستند. مثلا 0.05 یا 0.1 که به ترتیب برای آنها می‌توان گفت %95 و %90 تغییرات حفظ شده‌اند.

بنابراین اگر بخواهیم الگوریتم را بیان کنیم، به شکل زیر خواهد بود:

PCA را با $$k=1$$ امتحان کنید.
$U_{\text{reduce}}$ و $z^{(1)},...,z^{(m)}$ و $x_{\text{approx}}^{(1)},...,x_{\text{approx}}^{(m)}$ را محاسبه کنید.
بررسی کنید که آیا شرط زیر برقرار است؟

$$ \frac{\frac{1}{m}\sum_{i=1}^{m} {\lVert x^{(i)} - x^{(i)}_{\text{approx}} \rVert}^2}{\frac{1}{m} \sum_{i=1}^{m} {\lVert x^{(i)}\rVert}^2} \le 0.01 $$

اگر شرط مرحله ۳ برقرار بود، $$k=1$$ . در غیر اینصورت $$k=2$$ و پروسه را تکرار کنید. این روند تا زمان برقراری شرط مرحله ۳ ادامه داشته و از این طریق مقدار مناسب برای $$k$$ انتخاب می‌شود.

همانطور که معلوم است الگوریتم فوق بسیار ناکارآمد است. از آنجا که ممکن است نیاز باشد تا الگوریتم به تعداد مرتبه زیادی تکرار شود تا بتوان مقدار مناسب $$k$$ را پیدا کرد. ولی خوشبختانه در هنگام محاسبه PCA کمیتی را داریم که راه محاسبات گفته شده را بسیار آسان می‌کند. زمانی که از دستور

U,S,V = np.linalg.svd(Sigma)

استفاده می‌کنیم، ماتریس S را هم داریم که ماتریسی قطری به شکل زیر است:

$$ \begin{bmatrix} s_{11} & 0 & ... & 0 \\ 0 & s_{22} & ... & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & ... & s_{nn} \end{bmatrix} $$

و با داشتن این ماتریس می‌توان نسبت

$$ \frac{\frac{1}{m}\sum_{i=1}^{m} {\lVert x^{(i)} - x^{(i)}_{\text{approx}} \rVert}^2}{\frac{1}{m} \sum_{i=1}^{m} {\lVert x^{(i)}\rVert}^2} \le 0.01 $$

را بسیار ساده‌تر به شکل زیر محاسبه کرد:

$$ 1- \frac{\sum_{i=1}^{k}s_{ii}}{\sum_{i=1}^{n} s_{ii}} \le 0.01 $$

یا

$$ \frac{\sum_{i=1}^{k}s_{ii}}{\sum_{i=1}^{n} s_{ii}} \ge 0.99 $$

بنابراین کاری که باید برای انتخاب $$k$$ صورت گیرد به این شکل خواهد بود که کافی است مقدار $$k$$ را به تدریج افزایش دهیم و شرط بالا را بررسی کنیم.

ملاحظه می‌کنید با یکبار فراخوانی svd دیگر نیازی نیست که هر بار PCA را از اول محاسبه کنیم. پس به‌ صورت خلاصه برای انتخاب $$k$$ به شکل زیر عمل کنید:

U,S,V = np.linalg.svd(Sigma)
انتخاب کوچکترین مقدار k که برای آن شرط زیر برقرار باشد:

$$ \frac{\sum_{i=1}^{k}s_{ii}}{\sum_{i=1}^{n} s_{ii}} \ge 0.99 $$

توصیه‌هایی در به کارگیری الگوریتم PCA

یکی از کاربردهای الگوریتم PCA می‌تواند برای افزایش سرعت در یادگیری با نظارت باشد. برای مثال فرض کنید مسئله‌ای داریم که در آن $x^{(i)} \in \mathbb{R}^{10000}$ . یکی از مسائلی که در آن $x^{(i)} \in \mathbb{R}^{10000}$ می‌تواند مسئله دید کامپوتر (computer vision) باشد که در آن یک تصویر $100px \times 100px$ دارید. در چنین مواردی از هر کدام از الگوریتم‌های یادگیری با نظارت که بحث کرده‌ایم استفاده کنید، به لحاظ زمانی هزینه‌بر خواهند بود به عبارت دیگر اجرای آن‌ها زمان زیادی طول خواهد کشید. در چنین حالت‌هایی می‌توان از PCA کمک گرفت.

نحوه اجرای آن به صورت زیر است:

ابتدا از مجموعه داده خود $\{(x^{(1)},y^{(1)}),...,(x^{(m)},y^{(m)})\}$ ، تنها ورودی‌ها را جهت درست کردن یک مجموعه داده بدون برچسب استخراج می‌کنیم:

$$ x^{(1)},...,x^{(m)} \in \mathbb{R}^{10000} $$

اجرای PCA روی این داده‌ها و به دست آوردن مجموعه‌ای جدید مانند مجموعه زیر:
$$ z^{(1)},...,z^{(m)} \in \mathbb{R}^{1000} $$
بنابراین الان مجموعه داده‌ای جدید به شکل زیر خواهیم داشت:
$$\{(z^{(1)},y^{(1)}),...,(z^{(m)},y^{(m)})\}$$
استفاده از مجموعه داده به‌ دست آمده در الگوریتم مورد نظر (شبکه‌های عصبی یا هر یک از الگوریتم‌های یادگیری با نظارت مد نظر خود) و به‌ دست آوردن فرضیه.

توجه داشته باشید که اگر مثال جدیدی داشته باشید، باید آن را هم دقیقا بر اساس PCAایی که در مرحله 2 اجرا کرده‌اید، به خصوصیت جدید

\(z\)

تصویر کنید و سپس این خصوصیت را جهت پیش‌بینی به تابع فرضیه بدهید.

پس تا اینجا می‌توان کاربردهای PCA را به صورت زیر نوشت:

فشرده‌سازی:
- کاهش حافظه مورد نیاز برای ذخیره داده
- افزایش سرعت الگوریتم یادگیری
در این حالت انتخاب $k$ بر اساس درصدی از تغییرات که می‌خواهیم حفظ شود، صورت می‌گیرد.
به تصویر کشیدن: در این حالت چون تنها داده‌های دو بعدی و سه بعدی را می‌توان رسم کرد معمولا $$k = 2$$ یا $$k = 3$$ انتخاب می‌شود.

یک استفاده‌ بد از الگوریتم PCA برای جلوگیری از مسئله overfitting است. ممکن است استدلال کنید، اگر از PCA جهت کاهش تعداد خصوصیات استفاده کنم، با خصوصیات کمتر احتمال اتفاق افتادن overfitting هم کاهش می‌یابد. هر چند در واقعیت ممکن است که این کار جواب دهد ولی توصیه‌ ما این است که به جای استفاده از PCA جهت جلوگیری از overfitting از منظم سازی استفاده کنید:

$$\begin{eqnarray} \min_{\theta} \frac{1}{2m} &\sum&_{i=1}^{m} \left(h_{\theta}(x^{(i)}) - y^{(i)}\right)^2 \\ &\quad& + \frac{\lambda}{2m} \sum_{j=1}^{n} \theta^{2}_{j} \end{eqnarray}$$

زیرا PCA از برچسب یا همان متغیر $$y$$ استفاده نمی‌کند. در نتیجه ممکن است قسمتی از اطلاعات را برای کاهش بعد دور بریزد بدون آنکه بداند مقدار $$y$$ برای آن چیست؟ ضمن اینکه اگر قرار باشد بیش از %95 تغییرات را حفظ کنید معمولاً روش منظم‌سازی را‌ه‌حل بهتری برای جلوگیری از overfitting است، به عبارت دیگر نتایج بهتری ارائه می‌دهد.

نکته‌ی آخرآنکه ابتدا الگوریتم خود را با داده‌های اصلی و بدون استفاده از PCA اجرا کنید. اگر بعد از اجرای الگوریتم دلیلی برای استفاده از PCA داشتید (نیاز به حافظه بالا یا سرعت اجرا کم و ...) فقط آنگاه از الگوریتم PCA استفاده کنید.

<< مبحث قبلی مبحث بعدی >>