Anomaly Detection
یافتن بیهنجاری چیست؟
در این فصل میخواهیم در مورد مسئله یافتن بیهنجاری (Anomaly Detection) بحث کنیم. این مسئله در یادگیری بدون نظارت یکی از پر کاربردترین و رایجترین مسائل است. همچنین مسئله یافتن بیهنجاری هرچند جزو یادگیری بدون نظارت است ولی جنبههای زیادی از آن در تشابه با یادگیری با نظارت است.
برای توضیح آن به یک مثال رجوع میکنیم. فرض کنید یک تولید کننده موتور هواپیما هستید. چنانکه موتورهای شما در خط تولید حرکت میکنند، یک سری تست برای کنترل کیفیت و بی نقص بودن موتورها انجام میشود. در خلال این تستها شما یک سری خصوصیات را اندازهگیری میکنید، مانند:
گرمای تولید شده \(x_1 = \)
شدت لرزش \(x_2 = \)
.....
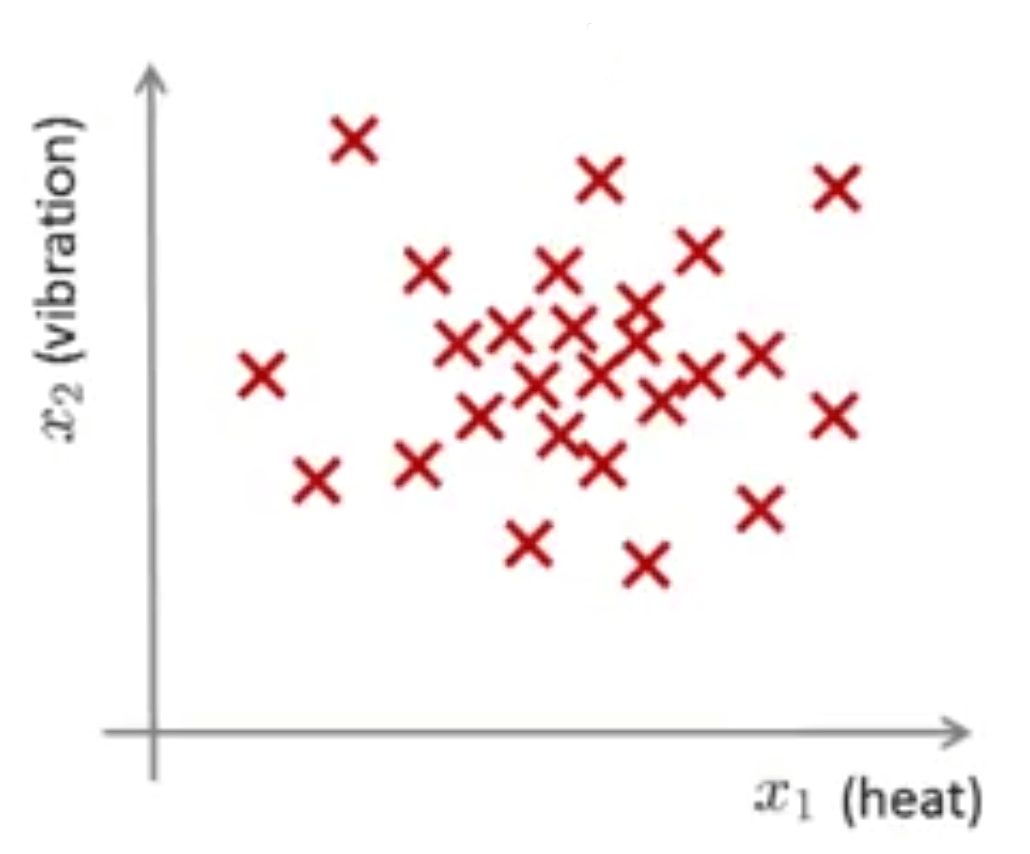
پس حالا یک مجموعه داده به مانند \(\{x^{(1)}, x^{(2)}, ..., x^{(m)}\}\) دارید که اگر آن را رسم کنید ممکن است نموداری شبیه زیر داشته باشیم.
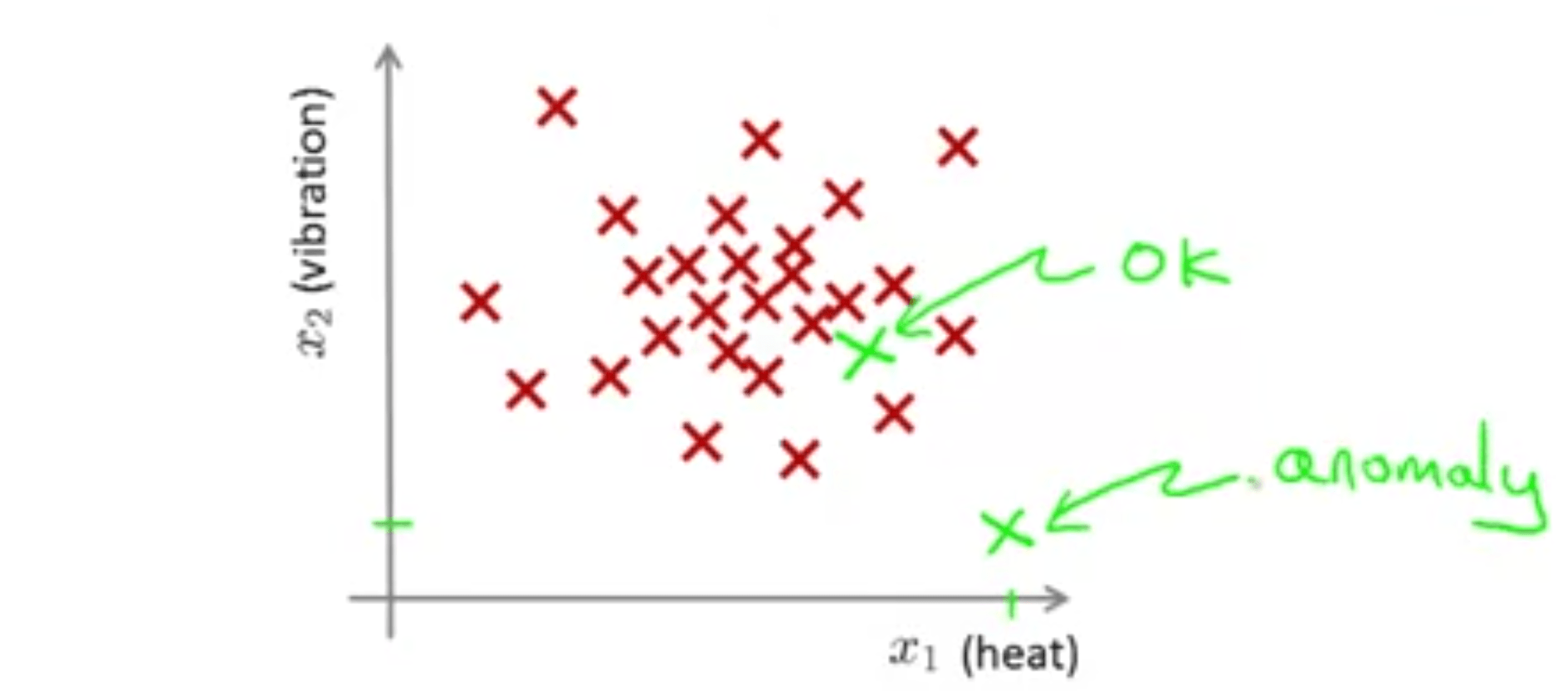
فرض کنید یک موتور هواپیمای جدید دارید \(x_{test}\) و این موتور در هنگام حرکت روی خط تولید برای آن یک سری خصوصیات اندازهگیری شده است. مسئله یافتن بیهنجاری به این صورت است که آیا این موتور هواپیمای جدید بیهنجار است یا خیر؟ به عبارت دیگر آیا این موتور نیاز به تستهای بیشتری برای اطمینان از عملکرد آن دارد و یا خیر؟
به عنوان مثال اگر بعد از رسم کردن خصوصیات موتور جدید، مقدار آن در نقطه سبز رنگ مشخص شده در میان نقاط قرمز رنگ قرار بگیرد، به نظر میرسد که موتور بدون عیب است و مشکلی جهت فرستادن به مشتری ندارد. ولی اگر در نقطه سبز رنگ پایین نموادر قرار بگیرد به نظر میرسد که با نمونههای سالم قبلی تفاوت زیادی دارد و بهتر است که آزمایشات بیشتری روی آن صورت گیرد تا از عملکرد درست آن اطمینان حاصل شود.
به صورت رسمیتر میتوان گفت که در مسئله یافتن بیهنجاری، یک مجموعه داده در اختیار ما قرار دارد که برابر نمونههای سالم هستند \(\{x^{(1)}, x^{(2)}, ..., x^{(m)}\}\) سپس یک نمونه جدید \(x_{test}\) به الگوریتم داده میشود و الگوریتم باید تشخیص دهد که آیا این نمونه جدید نرمال است یا بیهنجار. کاری که ما باید انجام دهیم ساختن یک مدل احتمالاتی \(p(x)\) است به صورتی که با دادن نمونه جدید به آن اگر \(p(x_{test}) \lt \epsilon\) (اپسیلون یک مقدار است که بعدا در مورد انتخاب آن بحث خواهیم کرد) الگوریتم آن را به عنوان بیهنجار شناسایی کند. به عبارت دیگر اگر \(p(x_{test}) \lt \epsilon\) باشد، میگوئیم احتمال وجود همچین نمونهای به عنوان نمونه نرمال بسیار کم است. در غیر اینصورت یعنی در حالت \(p_{(xtest)} \ge \epsilon\) میگوئیم که نمونه نرمال است.
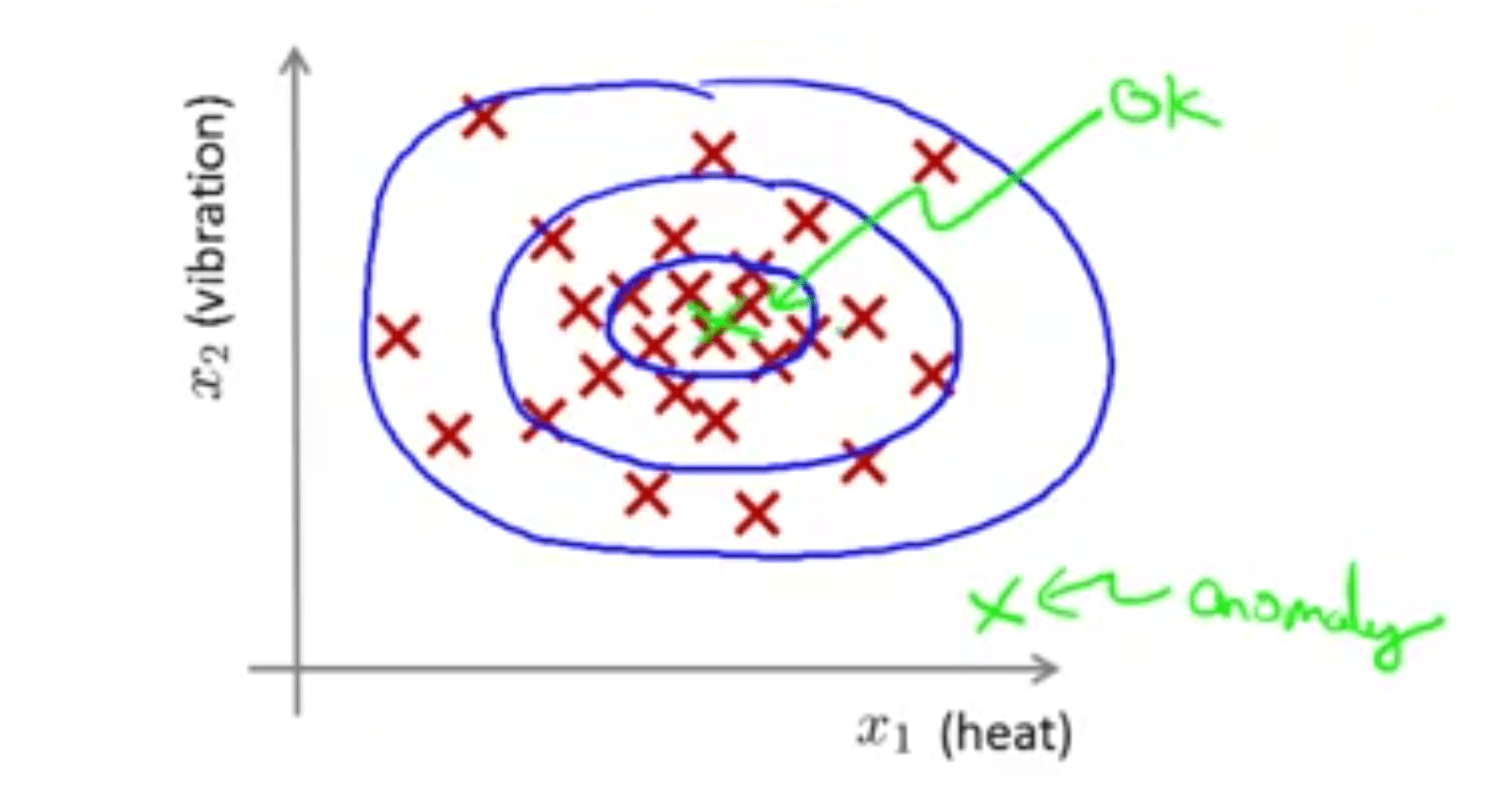
در شکل زیر هر چقدر از دایره مرکزی به سمت دایرههای بیرونی حرکت کنیم احتمال وجود نمونه نرمال کمتر میشود به طوریکه در نقطه سبز رنگ مشخص شده در گوشه سمت راست پایین نمودار احتمال بسیار کم است و به عبارتی این نمونه بیهنجار است.
مثالهایی از کاربرد یافتن بیهنجاری
یکی از کاربردهای رایج یافتن بیهنجاری، یافتن کلاهبرداری است (Fraud Detection). فرض کنید کاربرهای زیادی دارید (مثلاً کاربرهایی که به سایت شما مراجعه میکنند)، در این حالت، \(x(i)\) میتواند خصوصیت فعالیتهای کاربر iام باشد (تعداد ورود به سیستم، تعداد صفحاتی که مشاهده میکند و ...) بر اساس دادههای موجود، مدل احتمالاتی را برای آن به دست میآوریم و بر اساس این مدل کاربرهایی که غیرمعمول هستند را بوسیله \(p(x) \lt \epsilon\) چک و شناسایی میکنیم. مثال دیگر رسد کردن کامپیوترها در یک مرکز داده است. به این صورت که \(x(i)\) خصوصیات ماشین iام است. (\(x_1\) حافظه مورد استفاده، \(x_2\) تعداد دسترسی به دیسکها بر ثانیه، \(x_3\) بارگذاری CPU و ...) دوباره بر اساس دادههای موجود مدل احتمالاتی \(p(x)\) را درست کرده و سپس میتوان بر اساس این مدل کامپیوترهایی که به صورت غیرمعمول رفتار میکنند را شناسایی کرد.